Spiegazione teorica con i plugin di TeXmacs

Veniamo ora alla spiegazione teorica del motivo per cui l'arco principale dell'arcobaleno risulta visibile solo ad un angolo ben preciso di cui calcoleremo il valore. Indicati con x ed r rispettivamente l'angolo di incidenza e di rifrazione del raggio di luce monocromatica incidente la goccia è semplice dimostrare che, per il raggio di classe 3, la deflessione totale è pari a:

δ=π + 2 x - 4 r

da cui, utilizzando la legge dei seni di Cartesio, anche:

δ(x)=π + 2 x - 4 arcsin frac (sin x, n)

dove n≈1,33 indica l'indice di rifrazione dell'acqua. Possiamo, utilizzando il plugin di Gnuplot, rappresentare in TeXmacs il grafico della funzione δ(x):

set nokey

set size 0.8,0.8

set nolabel

set title "Deflessione Totale"

plot [0:pi/2] pi+2*x-4*asin(sin(x)/1.333)

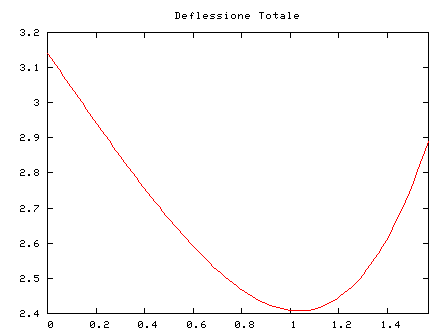
Dal grafico appare chiaro che la funzione deflessione al variare dell'angolo di incidenza, e quindi del parametro d'urto, inizilamente decresce, ha un minimo e poi cresce. Procediamo al calcolo del minimo lanciando il plugin del programma per il calcolo simbolico Maxima e determiniamo la derivata prima della deflessione:

(C1)

delta(x):=(Pi+2*x-4*asin(sin(x)/n));

(D11) δ(x):=π + 2 x + ( - 4) arcsin (frac (sin x, n))

(C12)

diff(delta(x),x)

(D12) 2 - frac (4 cos x, n sqrt (1 - frac (sin 2x, n2)))

Posto y=cos x possiamo calcolare gli zeri della derivata prima:

(C13)

g(y):=(16*y^2/(1.3335^2-1+y^2));

(D3) g(y):=frac (16 y2, 1.33352 - 1 + y2)

(C4)

solve(g(y)=4,y);

RAT replaced 0.77822225 by 11478//14749 = 0.77822225235609

(D4) [y= - frac (sqrt (3826), 7 sqrt (301)),y=frac (sqrt (3826), 7 sqrt (301))]

(C5)

%,numer;

(D5) [y= - 0.50932054489489,y=0.50932054489489]

(C6)

acos(0.50932);

(D13) 1.036401888781118

da cui si ottiene che il minimo della deflessione si ha in corrispondenza del valore:

xm≈1.0364 rad≈59 gradi.

Questo angolo minimo è quello a cui si osserva l'arco principale dell'arcobaleno. La ragione di ciò è la seguente: tutti i raggi che incidono la goccia con angoli in un intorno del minimo (punto stazionario) vengono deflessi di uno stesso angolo e quindi in corrispondenza dell'angolo di minimo si ha un massimo pronunciato di intensità. Al variare del colore dei raggi le considerazioni precedenti restano valide con l'avvertenza di modificare opportunamente il valore dell'indice di rifrazione. Per concludere osserviamo che dal momento che i raggi di un determinato colore sono deflessi complessivamente ad un determinato angolo essi si trovano su un cono che ha per asse la direzione incidente. Poiché quando si osserva l'arcobaleno si osserva una sezione conica si comprende anche il perché della sua forma curva.

© Copyleft 2004 Andrea Centomo