Figura 2.1.
[successivo] [precedente] [inizio] [fine] [indice generale]
Per rete logica o circuito logico si intende un circuito realizzato utilizzando dei componenti denominati porte logiche (alcune delle quali sono state già introdotte in 1.1).
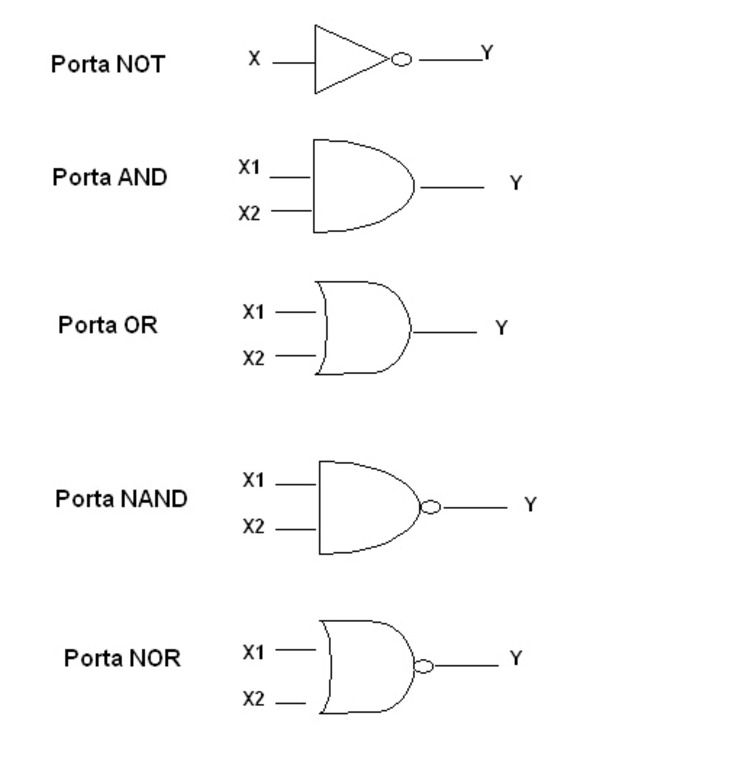
Nella figura 2.1 sono elencate le porte logiche più importanti.
|
Figura 2.1.
|
Ovviamente le variabili indicate a sinistra del simbolo grafico sono gli ingressi o input della porta logica, la variabile a destra è l'uscita o output.
In queste dispense ci limitiamo a considerare il caso di porte logiche con due soli ingressi; in generale però una porta logica può avere N ingressi.
La porta NAND si ottiene mettendo in serie una porta AND e una NOT; analogamente la NOR si ottiene mettendo in serie una porta OR e una NOT.
Quindi tali porte logiche non sono considerate fondamentali in quanto ottenute da combinazioni delle precedenti.
In realtà neanche NOT, AND e OR sono tutte fondamentali in quanto la AND si può sostituire con una combinazione di OR e NOT e la OR si può sostituire con una combinazione di AND e NOT.
Questo fatto è una diretta conseguenza delle leggi di De Morgan ed è illustrato nella figura 2.2.
|
Figura 2.2.
|
Sostituendo alle porte della figura i corrispondenti operatori logici si ottengono le stesse equivalenze come equivalenze tra espressioni logiche:
A^B ~ -(-A v -B)
AvB ~ -(-A ^ -B)
|
Questa operazione si può sempre fare in quanto ad ogni espressione logica è associato un circuito logico e viceversa; in pratica sono due formalismi diversi, uno simbolico e uno grafico, che rappresentano la stessa cosa: una combinazione di variabili logiche (o ingressi) e operatori logici (o porte) che forniscono un valore logico (o uscita). |
Ancora più interessante, almeno nell'ottica della realizzazione dei circuiti (reali e non logici) di un sistema di elaborazione, è il fatto che qualsiasi porta logica può essere sostituita da un circuito costituito da sole porte NAND oppure da sole porte NOR.
Nella figura 2.3 vengono rappresentati i circuiti con tutte NAND corrispondenti alle porte logiche fondamentali; equivalenze analoghe si possono ottenere utilizzando circuiti con tutte NOR.
|
Figura 2.3.
|
Le stesse equivalenze della figura in formule:
-A ~ -(A ^ A)
A^B ~ -( -(A ^ B) ^ -(A ^ B) )
AvB ~ -( -(A ^ A) ^ -(B ^ B) )
Un'ulteriore porta logica utile in molti casi è lo XOR o or esclusivo che si denota con il simbolo ± (in queste dispense, il simbolo "ufficiale" è invece come quello della OR però cerchiato).
Il circuito logico che lo rappresenta è nella parte destra in figura 2.4; nella parte sinistra abbiamo invece la sua rappresentazione sintetica.
|
Figura 2.4.
|
La tabella di verità della XOR è la seguente:
|
Una rete logica o un circuito logico si dicono combinatori se i valori delle uscite dipendono unicamente dai valori degli ingressi, si dicono invece sequenziali se i valori delle uscite dipendono dai valori degli ingressi e anche dallo stato del sistema.
Nel secondo caso si dice che il sistema "ha memoria" in quanto conserva dei valori che rappresentano il suo stato in ogni momento.
Nella figura 2.6 abbiamo un registro che è un esempio di circuito sequenziale.
|
Figura 2.6.
|
Il valore di ingresso X viene scritto nel registro quando l'operazione di scrittura è abilitata (W=1); la lettura del valore del registro ed il suo trasferimento in Y può invece avvenire in qualsiasi momento.
I circuiti elettronici che realizzano questa funzione sono i latch o i flip-flop; in generale, in un sistema di elaborazione tutti i circuiti che hanno funzione di memoria sono (ovviamente) di tipo sequenziale.
I circuiti che hanno funzione di calcolo o manipolazione di bit sono invece combinatori; fra questi possiamo citare:
demultiplexer, è un circuito a 1 ingresso e 2N uscite che invia il valore dell'ingresso alla i-esima uscita in funzione del valore i codificato attraverso N ulteriori ingressi di controllo;
multiplexer, è un circuito a 2N ingressi e 1 uscita che invia in uscita il valore dell'i-esimo ingresso in funzione del valore i codificato attraverso N ulteriori ingressi di controllo;
decodificatore, è un circuito a N ingressi e 2 N uscite che rende attiva (pone a 1) una delle uscite in funzione della configurazione dei bit presenti agli ingressi;
codificatore, è un circuito a 2N ingressi e N uscite che fornisce nelle uscite il valore che individua quale degli ingressi è attivo;
half-adder, è un circuito a 2 ingressi e 2 uscite che effettua la somma fra i 2 bit in ingresso, fornendo in uscita il valore della somma e il bit di riporto; questo circuito è illustrato in figura 2.7 e sotto è riportata la relativa tabella di verità.
|
Figura 2.7.
|
|
Come esempio di rete sequenziale vediamo invece in figura 2.9 una memoria associativa, cioè una memoria ad accesso casuale alla quale si può accedere non solo in base ad un indirizzo ma anche in base ai valori (chiavi) contenuti nelle celle della memoria.
|
Figura 2.9.
|
Il dispositivo a destra, indicato come MUX è un multiplexer; tutte le celle della memoria hanno un campo chiave e uno, o più, campi informazione; il valore da cercare (K) viene confrontato simultaneamente con tutte le chiavi tramite operazioni XOR:
se K non è presente, tutte le XOR danno risultato 1 e andando in input alla porta AND in alto si ottiene il risultato non trovato; inoltre tutti gli 1 vengono negati e arrivano come zeri al MUX che quindi non emette alcuna informazione;
se K è presente, una delle XOR (supponiamo quella con K2) da risultato 0, quindi la AND del Fault non è più vera e inoltre tale 0, grazie alle negazioni sulla sinistra, arriva come 1 in input al MUX provocando l'uscita dell'informazione INF2.
Il procedimento tramite il quale si passa dalla rappresentazione di una rete o di un circuito logico (o della relativa espressione logica) alla sua valutazione tramite la tabella di verità, prende il nome di analisi del circuito.
Il processo inverso si chiama sintesi del circuito e consiste nel risalire dai valori della tabella di verità ad uno dei possibili circuiti (o ad una delle possibili espressioni) ad essa associabili.
Si noti come il processo di sintesi possa condurre a molteplici soluzioni; ciò deriva dal fatto che di una funzione logica si possono avere molte rappresentazioni simboliche o grafiche in virtù delle equivalenze tra porte logiche esaminate in precedenza.
La sintesi di un circuito logico è meno banale dell'analisi; conviene senz'altro prima cercare un'espressione logica compatibile con la tabella di verità e poi eventualmente creare il relativo circuito.
Per trovare un'espressione logica associabile ad una tabella di verità ci sono sostanzialmente due metodi denominati somma di prodotti e prodotto di somme.
Nel primo caso si deve fare una OR (somma) tra i termini corrispondenti a valori 1 nella colonna del risultato della tabella; ognuno di tali termini è costituito dalla AND (prodotto) di tutti gli ingressi negati oppure no a seconda che in quella riga appaiano con valore 0 oppure 1.
Nel caso di prodotto di somme invece si deve fare una AND (prodotto) tra i termini corrispondenti a valori 0 nella colonna del risultato della tabella; ognuno di tali termini è costituito dalla OR (somma) di tutti gli ingressi negati oppure no a seconda che in quella riga appaiano con valore 1 oppure 0.
Si consideri ad esempio la seguente tabella di verità:
|
Il processo di sintesi effettuato con i due metodi ora illustrati condurrà rispettivamente alle seguenti espressioni logiche:
Y = -A^-B v A^B
Y = (Av-B) ^ (-AvB)
dalle quali si passa facilmente ai circuiti logici della figura 2.11.
|
Figura 2.11.
|
In precedenza è stato illustrato l'half-adder cioè il circuito che effettua la somma fra due bit fornendo il risultato e il riporto.
Per la somma tra valori costituiti da più bit occorre introdurre un circuito più complesso denominato sommatore binario; esso è costituito da un insieme di circuiti più semplici chiamati full-adder ognuno dei quali effettua la somma tra coppie di bit corrispondenti.
Il full-adder è a sua volta basato sull'half-adder ma, nel compiere la somma tra una coppia di bit, deve considerare anche l'eventuale riporto proveniente dalla coppia immediatamente a destra.
Un full-adder quindi è un circuito combinatorio con tre ingressi (i due bit ed il riporto «precedente») e due uscite (la somma ed il riporto «corrente» da passare alla coppia di bit adiacente a sinistra) come schematizzato in figura 2.12.
|
Figura 2.12.
|
Nella figura 2.13 viene invece mostrato più in dettaglio il circuito con l'uso di due half-adder (blocchi denominati H-A).
|
Figura 2.13.
|
Questa è la relativa tabella di verità:
|
Facendo la sintesi si ottengono le espressioni logiche che permettono di ricavare la somma e il riporto in uscita:
S = -A^-B^RP v -A^B^-RP v A^-B^-RP v A^B^RP RC = -A^B^RP v A^-B^RP v A^B^-RP v A^B^RP
Nella figura 2.15 viene infine mostrato un sommatore binario per operandi da 4 bit ottenuto combinando quattro full-adder; componendo opportunamente sommatori binari da 4 bit si possono poi ottenere sommatori binari per valori costituiti da un numero maggiore di bit (8, 16, 32 ecc.).
|
Figura 2.15.
|
Dovrebbe essere possibile fare riferimento a questa pagina anche con il nome reti_logiche.html