Capitolo 1. Pseudocodifica
Un tempo la programmazione avveniva attraverso lunghe fasi di studio a tavolino. Prima di iniziare il lavoro di scrittura del programma (su moduli cartacei che venivano trasferiti successivamente nella macchina) si passava per la realizzazione di un diagramma di flusso, o flow chart.
Il diagramma di flusso andava bene fino a quando si utilizzavano linguaggi di programmazione procedurali, come il COBOL. Quando si sono introdotti concetti nuovi che rendevano tale sistema di rappresentazione più complicato del linguaggio stesso, si è preferito schematizzare gli algoritmi attraverso righe di codice vero e proprio o attraverso una pseudocodifica più o meno adatta al concetto che si vuole rappresentare di volta in volta.
In questo capitolo viene presentata una pseudocodifica e alcuni esempi di algoritmi tipici, utilizzabili nella didattica della programmazione. Gli esempi proposti non sono ottimizzati perché si intende puntare sulla chiarezza piuttosto che sull'eventuale velocità di esecuzione.
1.1 Descrizione
La pseudocodifica utilizzata in questo capitolo si rifà a termini e concetti comuni a molti linguaggi di programmazione recenti. Vale la pena di chiarire solo alcuni dettagli:
-
le variabili di scambio di una subroutine (una procedura o una funzione) vengono semplicemente nominate a fianco del nome della procedura, tra parentesi, e ciò corrisponde a una dichiarazione implicita di quelle variabili con un campo di azione locale e con caratteristiche identiche a quelle usate nelle chiamate relative;
-
il trasferimento dei parametri di una chiamata alla subroutine avviene per valore, impedendo l'alterazione delle variabili originali;
-
per trasferire una variabile per riferimento, in modo che il suo valore venga aggiornato al termine dell'esecuzione di una subroutine, occorre aggiungere il simbolo @ di fronte al nome della variabile utilizzata nella chiamata;
-
il simbolo # rappresenta l'inizio di un commento;
-
il simbolo := rappresenta l'assegnamento;
-
il simbolo :==: rappresenta lo scambio tra due operandi.
1.2 Problemi elementari di programmazione
Nelle sezioni seguenti sono descritti alcuni problemi elementari attraverso cui si insegnano le tecniche di programmazione ai principianti. Assieme ai problemi vengono proposte le soluzioni in forma di pseudocodifica.
1.2.1 Somma tra due numeri positivi
La somma di due numeri positivi può essere espressa attraverso il concetto dell'incremento unitario: n + m equivale a incrementare m , di un'unità, per n volte, oppure incrementare n per m volte. L'algoritmo risolutivo è banale, ma utile per apprendere il funzionamento dei cicli.
SOMMA (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := X
FOR I := 1; I <= Y; I++
Z++
END FOR
RETURN Z
END SOMMA
In questo caso viene mostrata una soluzione per mezzo di un ciclo enumerativo, FOR. Il ciclo viene ripetuto Y volte, incrementando la variabile Z di un'unità. Alla fine, Z contiene il risultato della somma di X per Y. La pseudocodifica seguente mostra invece la traduzione del ciclo FOR in un ciclo WHILE.
SOMMA (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := X
I := 1
WHILE I <= Y
Z++
I++
END WHILE
RETURN Z
END SOMMA
1.2.2 Moltiplicazione di due numeri positivi attraverso la somma
La moltiplicazione di due numeri positivi, può essere espressa attraverso il concetto della somma: n * m equivale a sommare m volte n , oppure n volte m . L'algoritmo risolutivo è banale, ma utile per apprendere il funzionamento dei cicli.
MOLTIPLICA (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := 0
FOR I := 1; I <= Y; I++
Z := Z + X
END FOR
RETURN Z
END MOLTIPLICA
In questo caso viene mostrata una soluzione per mezzo di un ciclo FOR. Il ciclo viene ripetuto Y volte, incrementando la variabile Z del valore di X. Alla fine, Z contiene il risultato del prodotto di X per Y. La pseudocodifica seguente mostra invece la traduzione del ciclo FOR in un ciclo WHILE.
MOLTIPLICA (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := 0
I := 1
WHILE I <= Y
Z := Z + X
I++
END WHILE
RETURN Z
END MOLTIPLICA
1.2.3 Divisione intera tra due numeri positivi
La divisione di due numeri positivi, può essere espressa attraverso la sottrazione: n : m equivale a sottrarre m da n fino a quando n diventa inferiore di m . Il numero di volte in cui tale sottrazione ha luogo, è il risultato della divisione.
DIVIDI (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := 0
I := X
WHILE I >= Y
I := I - Y
Z++
END WHILE
RETURN Z
END DIVIDI
1.2.4 Elevamento a potenza
L'elevamento a potenza, utilizzando numeri positivi, può essere espresso attraverso il concetto della moltiplicazione: n ** m equivale a moltiplicare m volte n per se stesso.
EXP (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := 1
FOR I := 1; I <= Y; I++
Z := Z * X
END FOR
RETURN Z
END EXP
In questo caso viene mostrata una soluzione per mezzo di un ciclo FOR. Il ciclo viene ripetuto Y volte, e ogni volta la variabile Z viene moltiplicata per il valore di X, a partire da 1. Alla fine, Z contiene il risultato dell'elevamento di X a Y. La pseudocodifica seguente mostra invece la traduzione del ciclo FOR in un ciclo WHILE.
EXP (X, Y)
LOCAL Z INTEGER
LOCAL I INTEGER
Z := 1
I := 1
WHILE I <= Y
Z := Z * X
I++
END WHILE
RETURN Z
END EXP
La pseudocodifica seguente mostra una soluzione ricorsiva.
EXP (X, Y)
IF X = 0
THEN
RETURN 0
ELSE
IF Y = 0
THEN
RETURN 1
ELSE
RETURN N * EXP (N, Y-1)
END IF
END IF
END EXP
1.2.5 Radice quadrata
Il calcolo della parte intera della radice quadrata di un numero si può fare per tentativi, partendo da 1, eseguendo il quadrato fino a quando il risultato è minore o uguale al valore di partenza di cui si calcola la radice.
RADICE (X)
LOCAL Z INTEGER
LOCAL T INTEGER
Z := 0
T := 0
WHILE TRUE
T := Z * Z
IF T > X
THEN
# È stato superato il valore massimo.
Z--
RETURN Z
END IF
Z++
END WHILE
END RADICE
1.2.6 Fattoriale
Il fattoriale è un valore che si calcola a partire da un numero positivo. Può essere espresso come il prodotto di n per il fattoriale di n -1, quando n è maggiore di 1, mentre equivale a 1 quando n è uguale a 1. In pratica, n ! = n * ( n -1) * ( n -2)... * 1.
FATTORIALE (X)
LOCAL I INTEGER
I := X - 1
WHILE I > 0
X := X * I
I--
END WHILE
RETURN X
END FATTORIALE
La soluzione appena mostrata fa uso di un ciclo WHILE in cui l'indice I, che inizialmente contiene il valore di X-1, viene usato per essere moltiplicato al valore di X, riducendolo ogni volta di un'unità. Quando I raggiunge lo zero, il ciclo termina e X contiene il valore del fattoriale. L'esempio seguente mostra invece una soluzione ricorsiva che dovrebbe risultare più intuitiva.
FATTORIALE (X)
IF X == 1
THEN
RETURN 1
END IF
RETURN X * FATTORIALE (X - 1)
END FATTORIALE
1.2.7 Massimo comune divisore
Il massimo comune divisore tra due numeri può essere ottenuto sottraendo a quello maggiore il valore di quello minore, fino a quando i due valori sono uguali. Quel valore è il massimo comune divisore.
MCD (X, Y)
WHILE X != Y
IF X > Y
THEN
X := X - Y
ELSE
Y := Y - X
END IF
END WHILE
RETURN X
END MCD
1.2.8 Numero primo
Un numero intero è numero primo quando non può essere diviso per un altro intero diverso dal numero stesso e da 1, generando un risultato intero.
PRIMO (X)
LOCAL PRIMO BOOLEAN
LOCAL I INTEGER
LOCAL J INTEGER
PRIMO := TRUE
I := 2
WHILE (I < X) AND PRIMO
J := X / I
J := X - (J * I)
IF J == 0
THEN
PRIMO := FALSE
ELSE
I++
END IF
END WHILE
RETURN PRIMO
END PRIMO
1.3 Scansione di array
Nelle sezioni seguenti sono descritti alcuni problemi legati alla scansione di array. Assieme ai problemi vengono proposte le soluzioni in forma di pseudocodifica.
1.3.1 Ricerca sequenziale
La ricerca di un elemento all'interno di un array disordinato può avvenire solo in modo sequenziale, cioè controllando uno per uno tutti gli elementi, fino a quando si trova la corrispondenza cercata.
- Variabili
-
LISTA
È l'array su cui effettuare la ricerca.
X
È il valore cercato all'interno dell'array.
A
È l'indice inferiore dell'intervallo di array su cui si vuole effettuare la ricerca.
Z
È l'indice superiore dell'intervallo di array su cui si vuole effettuare la ricerca.
- Pseudocodifica iterativa
-
RICERCASEQ (LISTA, X, A, Z) LOCAL I INTEGER FOR I := A; I <= Z; I++ IF X == LISTA[I] THEN RETURN I END IF END FOR # La corrispondenza non è stata trovata. RETURN -1 END PRIMO - Pseudocodifica ricorsiva
-
RICERCASEQ (LISTA, X, A, Z) IF A > Z THEN RETURN -1 ELSE IF X == LISTA[A] THEN RETURN A ELSE RETURN RICERCASEQ (@LISTA, X, A+1, Z) END IF END IF END RICERCASEQ
1.3.2 Ricerca binaria
La ricerca di un elemento all'interno di un array ordinato può avvenire individuando un elemento centrale: se questo corrisponde all'elemento cercato, la ricerca è terminata, altrimenti si ripete nella parte di array precedente o successiva all'elemento, a seconda del suo valore e del tipo di ordinamento esistente.
Il problema posto in questi termini è ricorsivo. La pseudocodifica mostrata utilizza le stesse variabili già descritte per la ricerca sequenziale.
RICERCABIN (LISTA, X, A, Z)
LOCAL M INTEGER
# Determina l'elemento centrale dell'array.
M := (A + Z) / 2
IF M < A
THEN
# Non restano elementi da controllare: l'elemento cercato non c'è.
RETURN -1
ELSE
IF X < LISTA[M]
THEN
# Si ripete la ricerca nella parte inferiore.
RETURN RICERCABIN (@LISTA, X, A, M-1)
ELSE
IF X > LISTA[M]
THEN
# Si ripete la ricerca nella parte superiore.
RETURN RICERCABIN (@LISTA, X, M+1, Z)
ELSE
# M rappresenta l'indice dell'elemento cercato.
RETURN M
END IF
END IF
END IF
END RICERCABIN
1.4 Problemi classici di programmazione
Nelle sezioni seguenti sono descritti alcuni problemi classici attraverso cui si insegnano le tecniche di programmazione. Assieme ai problemi vengono proposte le soluzioni in forma di pseudocodifica.
1.4.1 Bubblesort
Il Bubblesort è un algoritmo relativamente semplice per l'ordinamento di un array, in cui ogni scansione trova il valore giusto per l'elemento iniziale dell'array stesso. Una volta trovata la collocazione di un elemento, si ripete la scansione per il segmento rimanente di array, in modo da collocare un altro valore. La pseudocodifica dovrebbe chiarire il meccanismo.
- Variabili
-
LISTA
A
È l'indice inferiore del segmento di array da ordinare.
Z
- Pseudocodifica iterativa
-
BSORT (LISTA, A, Z) LOCAL J INTEGER LOCAL K INTEGER # Scandisce l'array attraverso l'indice J in modo da collocare ogni # volta il valore corretto all'inizio dell'array stesso. FOR J := A; J < Z; J++ # Scandisce l'array attraverso l'indice K scambiando i valori # quando sono inferiori a quello di riferimento. FOR K := J+1; K <= Z; K++ IF LISTA[K] < LISTA[J] THEN # I valori vengono scambiati. LISTA[K] :==: LISTA[J] END IF END FOR END FOR END BSORT - Pseudocodifica ricorsiva
-
BSORT (LISTA, A, Z) LOCAL K INTEGER # L'elaborazione termina quando l'indice inferiore è maggiore o uguale # a quello superiore. IF A < Z THEN # Scandisce l'array attraverso l'indice K scambiando i # valori quando sono inferiori a quello iniziale. FOR K := A+1; K <= Z; K++ IF LISTA[K] < LISTA[A] THEN # I valori vengono scambiati. LISTA[K] :==: LISTA[J] END IF END FOR # L'elemento LISTA[A] è collocato correttamente, adesso si # ripete la chiamata della funzione in modo da riordinare # la parte restante dell'array. BSORT (@LISTA, A+1, Z) END IF END BSORT
1.4.2 Torre di Hanoi
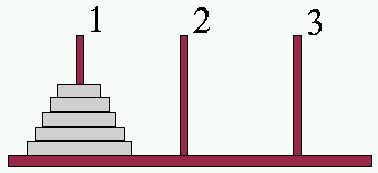
La torre di Hanoi è un gioco antico: si compone di tre pioli identici conficcati verticalmente su una tavola e di una serie di anelli di larghezze differenti. Gli anelli sono più precisamente dei dischi con un foro centrale che gli permette di essere infilati nei pioli.
Il gioco inizia con tutti gli anelli collocati in un solo piolo, in ordine, in modo che in basso ci sia l'anello più largo e in alto quello più stretto. Si deve riuscire a spostare tutta la pila di anelli in un dato piolo muovendo un anello alla volta e senza mai collocare un anello più grande sopra uno più piccolo.
|
Figura 1.1. Situazione iniziale della torre di Hanoi all'inizio del gioco. |
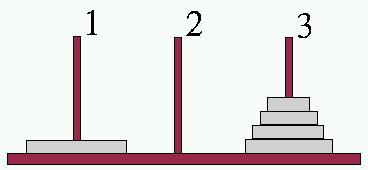
Nella figura 1.1 gli anelli appaiono inseriti sul piolo 1; si supponga che questi debbano essere spostati sul piolo 2. Si può immaginare che tutti gli anelli, meno l'ultimo, possano essere spostati in qualche modo corretto, dal piolo 1 al piolo 3, come nella situazione della figura 1.2.
|
Figura 1.2. Situazione dopo avere spostato n -1 anelli. |
A questo punto si può spostare l'ultimo anello rimasto (l' n -esimo), dal piolo 1 al piolo 2, e come prima, si può spostare in qualche modo il gruppo di anelli posizionati attualmente nel piolo 3, in modo che finiscano nel piolo 2 sopra l'anello più grande.
Pensando in questo modo, l'algoritmo risolutivo di questo problema deve essere ricorsivo e potrebbe essere gestito da un'unica subroutine che può essere chiamata opportunamente HANOI.
- Variabili
-
N
È la dimensione della torre espressa in numero di anelli: gli anelli sono numerati da 1 a N.
P1
È il numero del piolo su cui si trova inizialmente la pila di N anelli.
P2
È il numero del piolo su cui deve essere spostata la pila di anelli.
6-P1-P2
È il numero dell'altro piolo. Funziona così se i pioli sono numerati da 1 a 3.
- Pseudocodifica
-
HANOI (N, P1, P2) IF N > 0 THEN HANOI (N-1, P1, 6-P1-P2) scrivi: "Muovi l'anello" N "dal piolo" P1 "al piolo" P2 HANOI (N-1, 6-P1-P2, P2) END IF END HANOI - Descrizione
-
Se N, il numero degli anelli da spostare, è minore di 1, non si deve compiere alcuna azione. Se N è uguale a 1, le istruzioni che dipendono dalla struttura IF-END IF vengono eseguite, ma nessuna delle chiamate ricorsive fa alcunché, dato che N-1 è pari a zero. In questo caso, supponendo che N sia uguale a 1, che P1 sia pari a 1 e P2 pari a 2, il risultato è semplicemente:
Muovi l'anello 1 dal piolo 1 al piolo 2
che è corretto per una pila iniziale consistente di un solo anello.
Se N è uguale a 2, la prima chiamata ricorsiva sposta un anello (N-1 = 1) dal piolo 1 al piolo 3 (ancora assumendo che i due anelli debbano essere spostati dal primo al terzo piolo) e si sa che questa è la mossa corretta. Quindi viene stampato il messaggio che dichiara lo spostamento del secondo piolo (l'N-esimo) dalla posizione 1 alla posizione 2. Infine, la seconda chiamata ricorsiva si occupa di spostare l'anello collocato precedentemente nel terzo piolo, nel secondo, sopra a quello che si trova già nella posizione finale corretta.
In pratica, nel caso di due anelli che devono essere spostati dal primo al secondo piolo, appaiono i tre messaggi seguenti.
Muovi l'anello 1 dal piolo 1 al piolo 3 Muovi l'anello 2 dal piolo 1 al piolo 2 Muovi l'anello 1 dal piolo 3 al piolo 2
Nello stesso modo si potrebbe dimostrare il funzionamento per un numero maggiore di anelli.
1.4.3 Quicksort (ordinamento non decrescente)
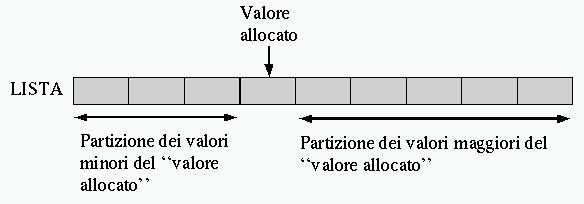
L'ordinamento degli elementi di un array è un problema tipico che si può risolvere in tanti modi. Il Quicksort è un algoritmo sofisticato, ottimo per lo studio della gestione degli array, oltre che per quello della ricorsione. Il concetto fondamentale di questo tipo di algoritmo è rappresentato dalla figura 1.3.
|
Figura 1.3. Il concetto base dell'algoritmo del Quicksort: suddivisione dell'array in due gruppi disordinati, separati da un valore piazzato correttamente nel suo posto rispetto all'ordinamento. |
Una sola scansione dell'array è sufficiente per collocare definitivamente un elemento (per esempio il primo) nella sua destinazione finale e allo stesso tempo per lasciare tutti gli elementi con un valore inferiore a quello da una parte, anche se disordinati, e tutti quelli con un valore maggiore, dall'altra.
In questo modo, attraverso delle chiamate ricorsive, è possibile elaborare i due segmenti dell'array rimasti da riordinare.
L'algoritmo può essere descritto grossolanamente come:
-
localizzazione della collocazione finale del primo valore, separando in questo modo i valori;
-
ordinamento del segmento precedente all'elemento collocato definitivamente;
-
ordinamento del segmento successivo all'elemento collocato definitivamente.
- Descrizione
-
Indichiamo con PART la subroutine che esegue la scansione dell'array, o di un suo segmento, per determinare la collocazione finale (indice CF) del primo elemento (dell'array o del segmento in questione).
Sia LISTA l'array da ordinare. Il primo elemento da collocare corrisponde inizialmente a LISTA[A], e il segmento di array su cui intervenire corrisponde a LISTA[A:Z] (cioè a tutti gli elementi che vanno dall'indice A all'indice Z).
Alla fine della prima scansione, l'indice CF rappresenta la posizione in cui occorre spostare il primo elemento, cioè LISTA[A]. In pratica, LISTA[A] e LISTA[CF] vengono scambiati.
Durante la scansione che serve a determinare la collocazione finale del primo elemento, PART deve occuparsi di spostare gli elementi prima o dopo quella posizione, in funzione del loro valore, in modo che alla fine quelli inferiori o uguali a quello dell'elemento da collocare si trovino nella parte inferiore, e gli altri dall'altra. In pratica, alla fine della prima scansione, gli elementi contenuti in LISTA[A:(CF-1)] devono contenere valori inferiori o uguali a LISTA[CF], mentre quelli contenuti in LISTA[(CF+1):Z] devono contenere valori superiori.
Indichiamo con QSORT la subroutine che esegue il compito complessivo di ordinare l'array. Il suo lavoro consisterebbe nel chiamare PART per collocare il primo elemento, continuando poi con la chiamata ricorsiva di se stessa per la parte di array precedente all'elemento collocato e infine alla chiamata ricorsiva per la parte restante di array.
Assumendo che PART e le chiamate ricorsive di QSORT svolgano il loro compito correttamente, si potrebbe fare un'analisi informale dicendo che se l'indice Z non è maggiore di A, allora c'è un elemento (o nessuno) all'interno di LISTA[A:Z] e inoltre, LISTA[A:Z] è già nel suo stato finale. Se Z è maggiore di A, allora (per assunzione) PART ripartisce correttamente LISTA[A:Z]. L'ordinamento separato dei due segmenti (per assunzione eseguito correttamente dalle chiamate ricorsive) completa l'ordinamento di LISTA[A:Z].
Le figure 1.4 e 1.5 mostrano due fasi della scansione effettuata da PART all'interno dell'array o del segmento che gli viene fornito.
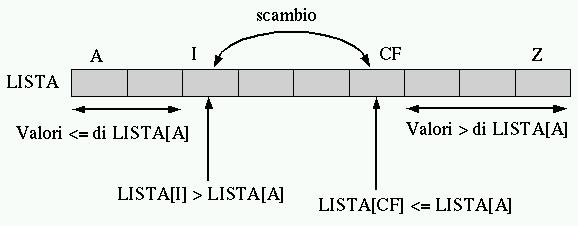
Figura 1.4. La scansione dell'array da parte di PART avviene portando in avanti l'indice I e portando indietro l'indice CF. Quando l'indice I localizza un elemento che contiene un valore maggiore di LISTA[A], e l'indice CF localizza un elemento che contiene un valore inferiore o uguale a LISTA[A], gli elementi cui questi indici fanno riferimento vengono scambiati, quindi il processo di avvicinamento tra I e CF continua.
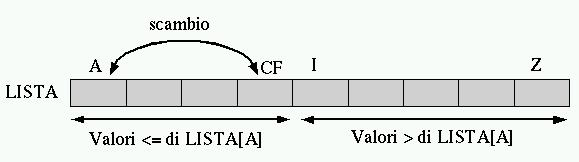
Figura 1.5. Quando la scansione è giunta al termine, quello che resta da fare è scambiare l'elemento LISTA[A] con LISTA[CF].
In pratica, l'indice I, iniziando dal valore A+1, viene spostato verso destra fino a che viene trovato un elemento maggiore di LISTA[A], quindi è l'indice CF a essere spostato verso sinistra, iniziando dalla stessa posizione di Z, fino a che viene incontrato un elemento minore o uguale a LISTA[A]. Questi elementi vengono scambiati e lo spostamento di I e CF riprende. Ciò prosegue fino a che I e CF si incontrano, momento in cui LISTA[A:Z] è stata ripartita e CF rappresenta la collocazione finale per l'elemento LISTA[L].
- Variabili
-
LISTA
L'array da ordinare in modo crescente.
A
L'indice inferiore del segmento di array da ordinare.
Z
L'indice superiore del segmento di array da ordinare.
CF
Sta per «collocazione finale» ed è l'indice che cerca e trova la posizione giusta di LISTA[L] nell'array.
I
- Pseudocodifica
-
PART (LISTA, A, Z) LOCAL I INTEGER LOCAL CF INTEGER # si assume che A < U I := A + 1 CF := Z WHILE TRUE # ciclo senza fine. WHILE TRUE # sposta I a destra IF (LISTA[I] > LISTA[A]) OR I >= CF THEN BREAK ELSE I := I + 1 END IF END WHILE WHILE TRUE # sposta CF a sinistra IF (LISTA[CF] <= LISTA[A]) THEN BREAK ELSE CF := CF - 1 END IF END WHILE IF CF <= I THEN # è avvenuto l'incontro tra I e CF BREAK ELSE # vengono scambiati i valori LISTA[CF] :==: LISTA[I] I := I + 1 CF := CF - 1 END IF END WHILE # a questo punto LISTA[A:Z] è stata ripartita e CF è la collocazione # di LISTA[A] LISTA[CF] :==: LISTA[A] # a questo punto, LISTA[CF] è un elemento (un valore) nella giusta # posizione RETURN CF END PART---------
QSORT (LISTA, A, Z) LOCAL CF INTEGER IF Z > A THEN CF := PART (@LISTA, A, Z) QSORT (@LISTA, A, CF-1) QSORT (@LISTA, CF+1, Z) END IF END QSORT
1.4.4 Permutazioni
La permutazione è lo scambio di un gruppo di elementi posti in sequenza. Il problema che si vuole analizzare è la ricerca di tutte le permutazioni possibili di un dato gruppo di elementi.
Se ci sono n elementi in un array, allora alcune delle permutazioni si possono ottenere bloccando l' n -esimo elemento e generando tutte le permutazioni dei primi n -1 elementi. Quindi l' n -esimo elemento può essere scambiato con uno dei primi n -1, ripetendo poi la fase precedente. Questa operazione deve essere ripetuta finché ognuno degli n elementi originali è stato usato nell' n -esima posizione.
- Variabili
-
LISTA
A
L'indice inferiore del segmento di array da permutare.
Z
L'indice superiore del segmento di array da permutare.
K
È l'indice che serve a scambiare gli elementi.
- Pseudocodifica
-
PERMUTA (LISTA, A, Z) LOCAL K INTEGER LOCAL N INTEGER IF (Z - A) >= 1 # Ci sono almeno due elementi nel segmento di array. THEN FOR K := Z; K >= A; K-- LISTA[K] :==: LISTA[Z] PERMUTA (LISTA, A, Z-1) LISTA[K] :==: LISTA[Z] END FOR ELSE scrivi LISTA END IF END PERMUTA