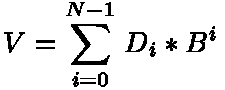
Il sistema di numerazione che usiamo comunemente è quello decimale, o in base 10, costituito dalle cifre da 0 a 9 e portato nel mondo occidentale durante il medioevo dai matematici arabi.
La proprietà fondamentale di questo sistema di numerazione e degli altri che ci accingiamo ad esaminare (binario, ottale, esadecimale) è quella di essere «posizionali»:
all’interno di un numero, ogni cifra assume un valore che dipende dal suo valore intrinseco e dalla sua posizione nel numero stesso.
Tutti infatti sappiamo che nel numero (decimale) 153, il 5 è nella posizione delle decine e vale cinquanta mentre nel numero 175 è nella posizione delle unità e vale cinque.
Connessa alla nozione di posizione di una cifra è quella di «peso»; con tale termine si indica un valore ottenuto facendo la potenza che ha per base la base del sistema di numerazione e per esponente il numero di cifre che, nel numero, stanno alla destra della cifra considerata.
Applicando questa definizione vediamo che nei numeri 153 e 175 la cifra 5 ha peso rispettivamente uguale a 10 e 1; quindi in pratica peso e posizione di una cifra sono la stessa cosa e si può parlare indifferentemente dell’uno o dell’altra.
Nella notazione posizionale è fondamentale il concetto di base di rappresentazione che indichiamo genericamente con B.
Il valore V di un numero composto da N cifre nella base B si può scrivere:
|
|
dove D0, D1, ..... DN-1 sono le cifre (comprese fra 0 e B-1) della stringa si simboli che rappresenta il numero.
Questa rappresentazione del valore di un numero si dice «polinomiale» perché ricalca la rappresentazione di un polinomio generico di grado N-1, con la B al posto dell'incognita X.
Il valore di un numero si può quindi ottenere facendo la somma dei prodotti fra le sue cifre e i rispettivi pesi.
A titolo di esempio consideriamo la rappresentazione polinomiale del numero decimale (B = 10) 836:
|
|
Il valore che si ottiene per V è ovviamente il già noto 836.
L'uso di questa rappresentazione, almeno per i numeri decimali, pare quindi di poca utilità; diviene però molto importante quando si usano sistemi di numerazione con altre basi, come mostrato più avanti.
Nel sistema di numerazione binario (o in base 2) si hanno a disposizione solo le due cifre 0 e 1.
Prima di procedere occorre stabilire una convenzione che permetta di distinguere i numeri binari da quelli decimali scritti con le stesse cifre; in mancanza di una regola certa infatti si creerebbero ambiguità come la seguente: 110 è il numero decimale centodieci o il numero binario uno - uno - zero?
Per risolvere il problema decidiamo di individuare i numeri binari con un due aggiunto a pedice di questi ultimi: 1102.
Il successivo problema che affrontiamo è quello delle conversioni tra basi diverse iniziando da quella da binario a decimale.
Supponiamo quindi di volere conoscere il valore rappresentato dal numero binario 11002; per fare questo ricorriamo alla rappresentazione polinomiale, che come visto in precedenza, permette di ottenere il valore di un numero:
|
|
Svolgendo i semplici calcoli otteniamo il valore 12.
Come ulteriore esempio convertiamo il numero binario 11001101112:
|
|
ottenendo il valore decimale 823.
Per effettuare la conversione inversa si deve usare un metodo leggermente meno banale denominato «algoritmo delle divisioni successive» che si origina dal seguente procedimento applicato alla rappresentazione polinomiale di un numero V in una base B:
|
|
ovvero:
|
|
che si può riscrivere come:
|
|
e quindi si può ricavare D0 come resto della divisione intera fra V e B.
Il quoziente di tale divisione è:
|
|
Su di esso si può iterare il procedimento per ricavare D1 e via via tutte le altre cifre arrestandosi quando il quoziente della divisione diviene zero.
Si deve osservare che in questo modo si ottengono le cifre da quella meno significativa a quella più significativa (da destra a sinistra).
Applichiamo l'algoritmo per convertire il valore decimale 86 in binario:
|
|
Quindi il valore binario ottenuto è 10101102.
Come ulteriore esempio convertiamo in binario il valore decimale 255:
|
|
ottenendo la rappresentazione binaria 111111112.
Essendo il bit l'unità fondamentale di misura della memoria, è importante chiedersi quante (e quali) sono le combinazioni diverse che si possono ottenere con N bit.
La risposta è in una semplice formula:
|
|
Dimostriamo la validità di questa formula con il procedimento di induzione:
si verifica sia vera per N=1;
si suppone che sia vera per N=K;
se si riesce dimostrare che è vera per N=K+1 allora è vera sempre.
Per N=1 la formula è vera perché con un bit si possono avere esattamente 2 combinazioni di valori: 0 e 1;
supposto sia vera per N=K abbiamo che:
|
|
e quindi è vera anche per N=K+1 e dunque per qualsiasi N.
Usando la formula possiamo quindi affermare che le combinazioni ottenibili con 4 bit sono 16 e, essendo un numero esiguo, le scriviamo anche per esteso con a fianco il relativo valore decimale:
|
|
Notiamo che i valori associati alle combinazioni sono quelli compresi tra 0 e 2N-1 (tra 0 e 15 con 4 bit) e anche questa formula è vera per qualsiasi valore di N.
I numeri binari non interi si rappresentano (in modo del tutto analogo ai decimali) con una parte intera, un punto e una parte frazionaria.
Il problema della conversione da binario a decimale di un numero non intero si risolve estendendo semplicemente la rappresentazione polinomiale di un numero anche alla parte non intera:
|
|
dove le Di sono le cifre della parte intera e le Fj quelle della parte frazionaria.
Quindi volendo convertire il numero binario 11010.1012 in decimale abbiamo:
|
|
da cui otteniamo il valore 26.625 .
Il problema della conversione inversa, da decimale a binario, può essere suddiviso in due sottoproblemi:
conversione della parte intera, con il già noto algoritmo delle divisioni successive;
conversione della parte frazionaria sulla quale ci concentriamo adesso.
Supponiamo di avere quindi un numero frazionario che possiamo esprimere come:
|
|
che si può riscrivere come:
|
|
quindi, se si moltiplica FRAZ per B, la parte intera del risultato risulta essere proprio la prima cifra frazionaria F1, mentre sulla parte frazionaria:
|
|
si può ripetere il procedimento per ottenere F2 e, iterando ancora, le altre cifre frazionarie.
Questo metodo si chiama «algoritmo delle moltiplicazioni successive» e si interrompe quando, dopo una moltiplicazione, si ottiene parte frazionaria pari a zero oppure quando si sono individuate un numero di cifre frazionarie ritenuto sufficiente ad esprimere il valore con la precisione desiderata.
Come esempio consideriamo la conversione del valore decimale 0.0625:
|
|
quindi 0.0625 = 0.00012.
Come esempio ulteriore convertiamo 32.87 stabilendo a priori di ottenere al massimo 6 cifre binarie frazionarie; il criterio di arresto (parte frazionaria pari a zero) non è infatti certo che sia soddisfatto dopo poche iterazioni e può anche non esserlo mai (infatti ci sono valori che hanno rappresentazione frazionaria finita in decimale ma non in binario).
Come detto in precedenza, in un caso come questo si convertono separatamente la parte intera e la parte frazionaria:
|
|
Il risultato finale è dunque: 32.87 = 100000.1101112.
Notiamo adesso che, se si riconverte in decimale il valore binario appena trovato, si ottiene 32.859375 che si discosta dal valore di partenza; il motivo è ovviamente che nella conversione da decimale non si sono trovate «abbastanza» cifre binarie frazionarie.
Nel caso dell'esempio precedente, invece, se riconvertiamo in decimale 0.00012 otteniamo il valore esatto 0.0625 e ciò si spiega con il fatto che il procedimento di calcolo delle cifre frazionarie si era arrestato regolarmente e non in modo forzato.
Nei sistemi di numerazione ottale e esadecimale (base 8 e base 16) sia hanno a disposizione rispettivamente otto e sedici cifre.
Nel sistema ottale non ci sono problemi nel decidere quali sono le otto cifre da usare: molto banalmente si considerano le prime otto cifre del sistema decimale, da 0 a 7.
Nel sistema esadecimale invece abbiamo il problema di individuare altri sei simboli da aggiungere alle cifre da 0 a 9; la scelta è quella di utilizzare le prime sei lettere dell'alfabeto inglese, A, B, C, D, E, F stabilendo il rispettivo valore intrinseco nel modo più ovvio:
|
|
Per quanto riguarda le conversioni da e verso valori decimali si applicano i metodi introdotti in precedenza: rappresentazione polinomiale e divisioni successive (non consideriamo valori ottali e esadecimali frazionari, quindi il metodo delle moltiplicazioni successive qui non serve); vediamo alcuni esempi.
Conversione del valore 137248 in decimale:
|
|
Conversione del valore F3B16 in decimale:
|
|
Conversione del valore 510 in ottale:
|
|
Quindi 510 = 7768.
Conversione del valore 3456 in esadecimale:
|
|
Quindi 3456 = D8016.
Le rappresentazioni R1 e R2 di uno stesso numero su basi B1 e B2 che sono una potenza dell'altra sono strettamente correlate:
se B1 = 2 e B2 = 2n, ogni cifra nella rappresentazione R2 corrisponde a n cifre nella rappresentazione R1.
In particolare:
ogni cifra ottale corrisponde a 3 cifre binarie;
ogni cifra esadecimale corrisponde a 4 cifre binarie.
Come conseguenza si ha un metodo per passare dalla rappresentazione di un numero in base B1 a quella in base B2 (o viceversa) senza applicare gli algoritmi di conversione; si può agire direttamente sostituendo ordinatamente ogni cifra di R1 con gruppi di n cifre di R2.
Vediamo alcuni esempi.
Conversione diretta di 4168 in binario:
|
|
Quindi 4188 = 1000011102.
Conversione diretta di A37C16 in binario:
|
|
Quindi A37C16 = 10100011011111002.
Conversione diretta di 10101101110112 in esadecimale e ottale:
10101101110112 = 0001 0101 1011 1011 = 15BB16
10101101110112 = 001 010 110 111 011 = 126738
L’interesse per i numeri esadecimali in informatica è dovuto al fatto che il computer gestisce i simboli 0 e 1 (bit) raggruppati in sequenze di otto cifre (byte) e che i codici più diffusi per la rappresentazione dei dati al suo interno sono lunghi otto bit; se si dividono a metà queste sequenze si ottengono gruppi di quattro cifre binarie (nibble) ognuno dei quali rappresenta una cifra esadecimale; risulta allora comodo esprimere i dati trattati dall'elaboratore attraverso i corrispondenti valori esadecimali.
Nei primi anni dell'informatica, fino agli anni '50, esistevano codici lunghi sei bit, quindi aveva un certo interesse la sequenza di sei cifre binarie il cui contenuto poteva essere rappresentato da due cifre ottali; ecco quindi che anche il sistema ottale riveste un ruolo importante nell'informatica, almeno per motivi «storici».
Queste considerazioni comunque non hanno molto interesse per gli utilizzatori dei computer, bensì per i programmatori o per i «tecnici» che hanno a che fare con la logica interna di funzionamento di tali macchine.
Essendo tutti i sistemi posizionali, le operazioni aritmetiche con numeri binari, ottali e esadecimali si svolgono con le regole già note nel sistema decimale.
Occorre però ricordare che il numero di cifre a disposizione cambia, così come il valore della base (anche se si scrive sempre con i simboli «10») e questo si ripercuote sui calcoli, in modo particolare sulle operazioni di «riporto» e di «presa a prestito».
Vediamo alcuni esempi limitandoci alle operazioni di somma e sottrazione.
Per sommare 1000112 e 101112 si incolonnano i due numeri a destra e si somma cifra per cifra a partire da destra ottenendo:
|
|
Per fare la sottrazione tra gli stessi due numeri si fa ancora l'incolonnamento e poi si sottrae cifra per cifra partendo da destra:
|
|
Passando a numeri ottali facciamo la somma e sottrazione tra 40478 e 2548:
Concludiamo con operazioni tra esadecimali sommando A9B16, FF316 e 9D16:
|
|
Infine facciamo la sottrazione tra B07316 e F9C16:
Non abbiamo fatto esempi sulle normali operazioni di moltiplicazione e divisione (che comunque non presentano alcuna novità a livello di metodo di calcolo), ma consideriamo un caso particolare di moltiplicazione e divisione: quelle che si ottengono mediante le operazioni di shift o scorrimento.
L'operazione di shift consiste nello spostare a destra o sinistra in un numero una certa quantità di cifre.
L'effetto di queste operazioni è il seguente:
shift verso sinistra di K cifre: si spostano le cifre di K posti a sinistra e le posizioni liberate si riempono con zeri; si ottiene la moltiplicazione del numero per BK (dove B ovviamente è la base del sistema di numerazione considerato);
shift verso destra di K cifre: si spostano le cifre di K posti a destra perdendo le K cifre meno significative; si ottiene la divisione intera tra il numero e BK.
In questo paragrafo vediamo alcune curiosità, anche storiche, sui numeri e sul loro uso.
Come abbiamo visto i «moderni» sistemi di numerazione sono tutti posizionali; nei tempi più antichi invece erano «addizionali».
Il più semplice si tali sistemi è quello basato su un solo simbolo: il trattino verticale |.
Ogni numero veniva rappresentato con tanti trattini quante erano le unità che lo costituivano.
Il sistema addizionale più famoso, ed in certi casi ancora utilizzato, anche se solo per motivi «coreografici», è invece quello dei numeri romani che si basa sui seguenti sette simboli:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
e sulle seguenti due regole:
se un simbolo ne segue un altro di valore uguale o maggiore, esso si somma al precedente;
se un simbolo ne precede un altro di valore maggiore, esso si sottrae dal successivo.
Ecco alcuni esempi di conversione da numero romano a valore decimale:
|
|
Se invece vogliamo convertire un valore decimale, ad esempio 27, in notazione romana, procediamo nel modo seguente:
27 è compreso fra 20 e 30 quindi scriviamo 20 in romano: XX;
la parte residua non rappresentata è 7 che è compreso fra 5 e 10 quindi scriviamo 5 in romano: V;
la parte residua non rappresentata è 2 che si rappresenta direttamente: II;
quindi in totale otteniamo: XXVII.
Nei sistemi di numerazione addizionali lo zero non ha senso di esistere; in effetti il suo utilizzo è diventato comune solo a partire dal secolo XIII, quando il matematico Pisano Leonardo Fibonacci lo introdusse nel mondo occidentale.
Questo avvenne unitamente all'introduzione del sistema di numerazione basato sulle cifre da 1 a 9, usato dagli Arabi, a loro volta ispirati dagli Indiani; grande merito a questo proposito va riconosciuto al matematico e astronomo persiano Muhammad Ibn Musa Al-Khwarizmi (considerato tra l'altro il «padre» dell'algebra) che nel secolo VIII introdusse la notazione posizionale e il concetto di zero.
Ancora oggi ci si riferisce alle cifre da 0 a 9 chiamandoli numeri «Arabi» o «Indo-Arabi».
Ci si può chiedere come mai tra tutti i sistemi di numerazione posizionali sia stato privilegiato quello decimale che oggi viene usato praticamente in tutto il Mondo.
Gli storici della matematica sono unanimi nel ritenere che ciò sia dovuto al fatto che l’uomo ha dieci dita e può usarle per contare.
Esistono però ancora tracce di sistemi di numerazione caduti in disuso e che forse avevano basi diverse dal dieci:
in molti contesti ha ancora una notevole importanza la «dozzina» come unità di misura; questa è una probabile reminiscenza di un sistema in base 12 per certi versi migliore del sistema decimale in quanto il 12 è divisibile per più fattori rispetto al 10;
i francesi per dire ottanta dicono «quattro volte venti»; questa è una probabile eredità di un vecchio sistema in base venti (o visegimale);
ancora oggi è usato, per misurare il tempo e gli angoli, il sistema di numerazione in base sessanta (o sessagesimale) degli antichi Babilonesi; il motivo per cui l’antico popolo della Mesopotamia scelse una base così «strana» è forse che il numero sessanta ha molti sottomultipli; si deve anche notare che il sistema dei Babilonesi era già posizionale ma non prevedeva il simbolo, e neppure il concetto, di zero.
Concludiamo con una nota «filosofica» riguardante i numeri binari.
Essi sono stati a lungo materia di studio e curiosità per molti matematici, anche famosi, che ammiravano la loro «eleganza» e semplicità; in particolare Leibnitz (1646 - 1716) vedeva nell’aritmetica binaria un’immagine della creazione: immaginava che l’unità rappresentasse Dio e lo zero il nulla e che Dio avesse creato tutti gli esseri dal nulla così come l’unità e lo zero esprimono tutti i valori nel sistema binario.