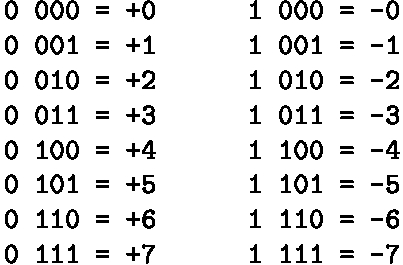
In tutti gli elaboratori elettronici costruiti fino ad oggi le informazioni sono rappresentate, trasmesse ed elaborate tramite grandezze fisiche, delle quali vengono considerati significativi solo alcuni valori (livelli discreti).
Se ad ogni livello si associa un simbolo diverso si ottiene un alfabeto per esprimere le informazioni da trattare.
Negli elaboratori si usa un alfabeto costituito dai due soli simboli 0 e 1, chiamati bit (BInary digiT), in quanto si preferisce avere a che fare con grandezze fisiche che hanno solo due livelli discreti e stabili.
I motivi di questa scelta si possono così riassumere:
efficienza: i calcoli sono svolti più rapidamente in binario che con altre basi di numerazione;
economicità: i dispositivi a due soli stati sono più semplici e meno costosi;
affidabilità: essendo solo due gli stati possibili delle grandezze fisiche è più semplice individuare errori di rappresentazione dovuti ai disturbi che esse subiscono («rumore» ambientale).
Rimandando maggiori dettagli e definizioni generali riguardanti i codici al paragrafo (3.2.1) in cui si esaminano le codifiche dei dati alfanumerici per l'elaboratore, vediamo adesso come si rappresentano in quest'ultimo le informazioni numeriche.
In questo capitolo vengono esaminati i principali metodi con i quali possono essere rappresentati i valori numerici all'interno del sistema di elaborazione distinguendo tra valori interi e valori reali.
In entrambi i casi è però importante chiarire come non ci si riferisca all'insieme dei numeri interi e all'insieme dei numeri reali conosciuti in matematica in quanto questi due insiemi sono infiniti (e quello dei reali è anche «denso», dato che tra valori vicini quanto si vuole, ci sono infiniti valori reali).
Data la finitezza dei componenti interni della macchina, non è possibile gestire infiniti valori e quindi si rappresentano solo dei sottoinsiemi dei numeri interi e dei numeri reali; inoltre quelli che fra questi ultimi hanno una rappresentazione infinita, possono essere solo approssimati.
In base a tali considerazioni sarebbe più corretto parlare di numeri interi macchina e numeri reali macchina quando si fa riferimento ai valori rappresentati nell'elaboratore; in queste dispense si fa comunque uso delle definizioni più brevi dando per scontato si intende parlare dei sottoinsiemi gestibili dalla macchina.
I metodi per la rappresentazione dei numeri interi nell'elaboratore sono fondamentalmente tre:
modulo (valore assoluto) e segno;
metodo dell'eccesso o bias (polarizzazione);
complemento a due.
Viene usato il bit più a sinistra, cioè il più significativo o MSB (Most Significant Bit) per indicare esplicitamente il segno con la seguente convenzione (che è quasi sempre valida anche in altri contesti):
0 = segno positivo;
1 = segno negativo.
Gli altri bit disponibili sono utilizzati per rappresentare il valore assoluto come numero binario «puro».
L'intervallo dei valori rappresentabili con N bit è:
-2(N-1)-1 <= X <= +2(N-1)-1
La quantità di valori è comunque 2N (come è lecito attendersi) e non 2N-1 , come appare dall'ampiezza dell'intervallo, perché ci sono due rappresentazioni del valore zero.
Se supponiamo ad esempio che i bit a disposizione per la gestione dei valori interi siano quattro (ovviamente tal valore è irrealisticamente basso, in realtà si hanno rappresentazioni con 8 o, meglio ancora, 16 o 32 bit) otteniamo i seguenti valori interi:
|
|
Osserviamo che il segno è completamente disgiunto dal valore assoluto e che, in linea di principio, la posizione del bit di segno entro la stringa di bit è irrilevante (ma si preferisce scegliere il bit più a sinistra).
Notiamo anche che, come detto, il valore zero ha due rappresentazioni e che non si possono usare i metodi usuali per eseguire le operazioni aritmetiche; addirittura non è vero che:
X + (-X) = 0
Infatti, facciamo 3 + (-3):
|
|
Il problema è proprio nel fatto che il bit del segno è disgiunto dal resto della rappresentazione e quindi deve essere trattato a parte nei calcoli.
Ciò rende necessari circuiti specifici o software più complessi per la realizzazione delle operazioni aritmetiche da parte della macchina e quindi, pur trattandosi di un metodo semplice e intuitivo, ha un uso concreto molto scarso.
Per usare questo metodo occorre prima di tutto calcolare il valore dell'eccesso o bias.
Supponendo che N sia il numero di bit disponibili per la rappresentazione dei valori, il calcolo si può fare in due modi:
bias = 2(N-1)
bias = 2(N-1)-1
Il numero X da rappresentare viene prima sommato al bias e poi tradotto in binario, in modo che sia sempre positivo; viceversa se abbiamo una rappresentazione binaria, dobbiamo sottrarre il bias al valore rappresentato per avere il valore effettivo.
Come esempio supponiamo di avere ancora quattro bit bit a disposizione; in tal caso il bias vale 8 oppure 7 i valori rappresentati nei due casi sono:
L'intervallo dei valori rappresentabili con N bit è:
-2(N-1) <= X <= +2(N-1)-1
oppure:
-2(N-1)-1 <= X <= +2(N-1)
in dipendenza di come viene calcolato il valore di polarizzazione.
Anche stavolta il primo bit rappresenta il segno, ma, contrariamente alla convenzione più diffusa, i numeri negativi hanno il bit del segno pari a 0 e i numeri positivi pari a 1; il valore zero ha 1 come bit del segno nella rappresentazione eccesso 2(N-1) e 0 nella rappresentazione eccesso 2(N-1)-1.
Questo metodo di rappresentazione è meno intuitivo del precedente, non è usato effettivamente per gestire i valori interi ma viene «ripescato» a proposito di un aspetto riguardante i numeri reali.
Vediamo prima di tutto come si definisce il complemento alla base B di un valore espresso, con N cifre, appunto, nella base B:
|
|
Ad esempio il complemento a dieci di 753 è 247 e possiamo vedere che si può ottenere, oltre che con l'applicazione della formula, anche facendo il complemento a nove di ogni singola cifra e sommando 1 al risultato.
Questa osservazione è molto utile per fare il complemento a due di un valore binario.
Supponiamo ad esempio di volerlo calcolare per il valore 1100102; possiamo applicare la definizione ottenendo:
|
|
ma in modo più agevole possiamo fare il complemento a uno di ogni cifra (che consiste banalmente nello scambiare i valori zero con uno e viceversa) e poi sommare 1:
|
|
|
Un altro metodo, ancora più semplice e veloce per ottenere il complemento a due di un numero binario è il seguente: «scorrere il numero da destra lasciando i bit inalterati fino al primo uno (compreso) e invertire il valore dei successivi bit». |
Anche con il metodo del complemento a due il bit più significativo rappresenta il segno, stavolta rispettando la convenzione più diffusa:
0 = segno positivo;
1 = segno negativo.
La regola generale per questa rappresentazione è la seguente:
se il valore è positivo lo si rappresenta normalmente in binario avendo però cura di scrivere anche gli zeri non significativi a sinistra (in modo che sia sempre presente il bit del segno);
se il valore è negativo si converte in binario e poi si effettua il complemento a due.
Facciamo due esempi per i valori 61 e -76, supponendo di avere a disposizione otto bit per la rappresentazione degli interi:
|
|
Quindi: 61 = 001111012.
|
|
Allora 76 sarebbe 010011002 e passando al complemento a due otteniamo: -76 = 101101002.
Per la conversione inversa, da binario espresso in complemento a due a decimale, si può procedere in due modi:
se il valore è positivo lo si converte normalmente; se è negativo prima si fa il complemento, poi lo si converte, infine si moltiplica il risultato per -1;
si converte normalmente il valore considerando però il peso del bit più significativo con esponente negativo.
Vediamo esempi dei due metodi considerando numeri negativi in quanto più «interessanti» e supponendo di avere 10 bit per la rappresentazione.
Convertiamo 10101100102; il complemento a due è: 01010011102 che passiamo in decimale:
|
|
quindi il risultato è: -334.
Convertiamo ora 11100011012 con l'altro metodo:
|
|
Come si vede il secondo metodo è molto più rapido.
La rappresentazione degli interi in complemento a due è senza dubbio la più utilizzata in quanto, pur essendo meno intuitiva di quella in modulo e segno ha i seguenti pregi:
si possono usare le regole dell'aritmetica binaria senza segno;
c'è una sola rappresentazione dello zero;
la convenzione sul bit del segno è rispettata;
non è necessario nessun circuito particolare per trattare i valori negativi;
è verificata la proprietà X + (-X) = 0 scartando però il bit di riporto che si ottiene a sinistra del bit del segno.
Vediamo un esempio relativo all'ultima osservazione supponendo che X sia 3 e che si usino quattro bit per scrivere i valori interi:
|
|
L'intervallo dei valori rappresentabili in complemento a due con N bit è:
-2(N-1) <= X <= +2(N-1)-1
Il massimo intero positivo rappresentabile è in modulo inferiore di uno al minimo negativo rappresentabile perché il valore zero fa intrinsecamente parte dei valori positivi.
Se supponiamo che N sia 4, vediamo quali sono i valori rappresentati:
|
|
Si noti che con questo tipo di notazione si perde la «somiglianza» tra valori opposti che invece c'era nella rappresentazione in modulo e segno; questo però non è un problema perché per il sistema di elaborazione tale perdita non porta alcuno svantaggio.
La rappresentazione in complemento a due è la più utilizzata anche per un motivo legato ai calcoli aritmetici: la sottrazione tra due valori espressi in questa forma può infatti essere effettuata comodamente facendo una somma tra il primo valore ed il complemento a due del secondo (scartando il bit di riporto oltre il bit del segno).
A dire il vero il «trucco» è sfruttabile anche in decimale facendo la somma tra il primo valore ed il complemento a dieci del secondo; ad esempio:
per fare 842 - 245 facciamo 842 + 755 ottenendo = 1597 e, scartando il primo 1, abbiamo 597 che è il risultato atteso.
Il fatto che le sottrazioni si trasformino in somme è molto importante ai fini della semplificazione dei circuiti interni del sistema di elaborazione in quanto non sono necessari dispositivi adibiti a svolgere queste operazioni.
Se poi si tiene conto che le moltiplicazioni si possono ottenere «via software» come successioni di somme e le divisioni analogamente come successioni di sottrazioni, emerge che l'unico circuito aritmetico necessario alla macchina è, almeno in linea teorica, il circuito sommatore.
Nello svolgere le operazioni di somma e sottrazione occorre però porre attenzione agli errori che si possono verificare e che sono dovuti alla limitatezza dell'intervallo dei valori rappresentabili.
Si possono infatti verificare situazioni di overflow o traboccamento dovute la fatto che il risultato di una operazione esce da tale intervallo.
Ci sono vari sistemi per accorgersi di questo tipo di errori:
la somma tra due valori positivi pare fornire un risultato negativo o comunque il segno del risultato è opposto a quello che sarebbe lecito attendersi;
esaminando i valori coinvolti nell'operazione ci si accorge che il risultato eccede i limiti dei valori rappresentabili prima ancora di svolgere l'operazione;
si riscontra una situazione particolare relativamente al riporto sul bit del segno e sul bit ulteriore a sinistra di quello del segno.
Chiariamo meglio l'ultimo punto:
se si ha un riporto sul bit del segno e sul bit a sinistra di esso, oppure, non si ha riporto su nessuno dei due bit, allora il risultato è corretto (scartando l'eventuale bit eccedente a sinistra dal risultato);
se si ha un riporto sul bit del segno e non sul bit a sinistra di esso o viceversa, allora il risultato non è corretto e si ha una situazione di overflow.
Vediamo alcuni esempi in cui si suppone di avere a disposizione otto bit per la rappresentazione dei valori interi (per brevità le conversioni non vengono dettagliate).
somma tra -50 e +90:
|
|
differenza tra -50 e +90 (fatta come somma tra -50 e il complemento di +90):
|
|
somma tra 84 e -75:
|
|
differenza tra 84 e -75 (fatta come somma tra 84 e il complemento di -75):
|
|
somma tra 55 e 99:
|
|
differenza tra 55 e 99 (fatta come somma tra 55 e il complemento di 99):
|
|
A causa della limitatezza dei dispositivi dedicati alla rappresentazione dei valori interi macchina, per essi non valgono la proprietà associativa e commutativa della somma e del prodotto e la proprietà distributiva della somma.
Infatti se ad esempio X è il massimo intero rappresentabile, l'espressione (X-X)+X (che, calcolata, dà il risultato corretto pari a X) non equivale a X-(X+X), in quanto il risultato parziale (X+X) non è rappresentabile.
Nell'elaboratore, oltre che di aritmetica finita, si parla anche di aritmetica modulare in cui i numeri interi «si avvolgono su se stessi» e si possono rappresentare su una circonferenza anziché sulla usuale retta infinita.
Notiamo infatti che se si dedicano sedici bit alla rappresentazione dei valori interi (come per gli interi in linguaggio Pascal) si ha un intervallo di valori compreso tra -32.768 e +32.767 ma, al di fuori di esso non c'è il «vuoto» in quanto, essendo i valori disposti su una circonferenza, dopo il valore 32.767 si troverà il valore -32.768, poi -32.767 e così via.
Aumentando il numero di bit a disposizione si amplia ovviamente l'intervallo dei valori rappresentabili: con trentadue bit (valori interi per il linguaggio c) si va da -2.147.483.648 a 2.147.483.647; rimane però valido il concetto di disposizione «circolare» di tali valori.
Abbiamo già accennato al fatto che la rappresentazione finita dei reali nel calcolatore è impossibile quando i numeri hanno infinite cifre nella parte frazionaria; questo accade per:
numeri irrazionali, non rappresentabili finitamente in forma esplicita in nessuna base (ad esempio: 21/2, π);
numeri razionali periodici nella base di rappresentazione utilizzata.
A tale proposito si deve notare che un valore razionale può essere periodico o meno a seconda della base usata per rappresentarlo; ad esempio 1/3 = 0.333333333333... è periodico in base 10 ma non in base 3 dove si scrive 0.13, oppure 8/7 = 1.142857142857... periodico in base 10 ma non in base 7 dove si scrive 1.17.
In generale abbiamo che se un valore è periodico quando rappresentato in base B, lo è anche quando rappresentato in qualunque base B1 che sia un fattore di B (B = k*B1).
Quindi se X è periodico in base 10, lo è anche in base 2 o in base 5 (ma non vale necessariamente il viceversa).
Inoltre abbiamo che se un valore è periodico in base B lo è anche in una base B2 che è una sua potenza (B2 = Bk).
Quindi se Y è periodico in base 2 lo è anche in base 8 e 16.
La rappresentazione in virgola fissa è così denominata in quanto, stabilito il numero K di bit da usare per memorizzare i numeri reali (valori possibili di k sono: 16, 32, 64, 80), si usano:
un bit per rappresentare il segno;
i rimanenti K-1 bit per la memorizzazione della parte intera e della parte frazionaria, suddividendoli in due gruppi di ampiezza fissa (la virgola di separazione tra parte intera e frazionaria assume idealmente una posizione fissa).
Supponiamo ad esempio che i bit a disposizione in una ipotetica macchina siano 32 e che la suddivisione sia: 1 per il segno, 15 per la parte intera e 16 per la parte frazionaria; in questo caso avremmo un intervallo di valori rappresentabili compreso tra 0.1*2-16 e 215 per i valori positivi ed uno analogo per i valori negativi.
Questo metodo di rappresentazione dei numeri reali macchina non è conveniente in quanto i valori rappresentabili sono relativamente pochi e la precisione che si ottiene non è elevata.
La rappresentazione in virgola mobile (floating point), detta anche a mantissa e caratteristica, si basa sulla notazione esponenziale o scientifica dei numeri.
Secondo tale notazione un numero reale può essere espresso nella seguente forma:
|
|
dove:
m è un valore frazionario chiamato mantissa;
B è la base del sistema di numerazione;
esp è un valore intero chiamato esponente o caratteristica.
Ad esempio il valore 1.125 lo possiamo rappresentare come 1.125*100 ma anche come 0.1125*101 oppure come 11.25*10-1.
In effetti, data una base B, esistono infinite coppie (m, esp) in grado di rappresentare, lo stesso valore reale V.
Questo fatto, in vista della definizione di uno standard che sia universale per la rappresentazione dei reali macchina e che elimini le ambiguità, non è molto positivo; occorre dunque fare una scelta tra le varie forme esponenziali, in modo che la rappresentazione di un dato valore sia unica.
La scelta ricade sulla notazione esponenziale normalizzata che è quella per cui la mantissa è compresa tra 0 (incluso) e 1 (escluso) e la sua prima cifra (se il valore di m non è zero) è diversa da zero.
Tornando all'esempio precedente la notazione esponenziale normalizzata (che è univoca) è 0.1125*101.
Osserviamo che, nel caso di valore normalizzato, vale:
|
|
Infatti, ricordando che m è un numero frazionario, abbiamo:
|
|
pertanto affinché in qualunque base la prima cifra della mantissa sia diversa da zero deve esserci il termine F1*B-1 e quindi si ha che 1/B < m.
La rappresentazione normalizzata è una scelta efficiente perché sfrutta tutte le cifre disponibili per la mantissa senza sprecarle per zeri iniziali che non portano vera informazione.
Nell'elaboratore la rappresentazione di valori reali è espressa ovviamente in binario, quindi dobbiamo preoccuparci di convertire dei valori reali decimali in binario con notazione esponenziale normalizzata.
Per fare questo si può convertire il valore decimale V in binario (separatamente per la parte intera e la parte frazionaria, come visto in precedenza) e poi normalizzare il valore ottenuto.
Esiste però anche un metodo alternativo:
individuare le potenze di 2 tra le quali si trova V;
prendere la più alta delle due ed assegnare l'indice della potenza all'esponente esp;
assegnare alla mantissa m il risultato della seguente operazione:
|
|
convertire in binario la mantissa m così ottenuta.
Ad esempio troviamo la rappresentazione normalizzata in base 2 di 5.875:
siccome 22 < 5.875 < 23 abbiamo esp = 3
m = 5.875/8 = 0.734375
convertiamo 0.734375 in binario:
Quindi: 5.875 = 0.1011112*23.
Nella storia dell'informatica c'è stato un periodo in cui ogni grande azienda proponeva il suo metodo di rappresentazione dei valori reali in virgola mobile senza curarsi dei problemi di compatibilità dei dati.
Per porre fine alla proliferazione dei formati di rappresentazione fu proposto uno standard dallo IEEE (Institute of Electrical and Electronics Engineers) denominato IEEE 754 o Standard for Binary Floating-Point Arithmetic.
Lo standard definisce tre formati:
singola precisione (single precision) con utilizzo di 32 bit;
doppia precisione (double precision) con utilizzo di 64 bit;
precisione estesa (extended precision) con utilizzo di 80 bit.
La precisione estesa è comunque usata solo internamente alle unità di calcolo FPU (Floating Point Unit) e non viene messa a disposizione per la definizione dei dati da parte dei linguaggi di programmazione.
In tutti e tre i formati le informazioni che vengono gestite per memorizzare i valori reali sono:
segno del numero;
mantissa del numero;
caratteristica del numero.
Il numero viene considerato espresso in binario secondo la notazione esponenziale che qui chiamiamo per comodità «quasi normalizzata».
Non viene utilizzata la forma normalizzata in quanto in essa il primo bit frazionario vale sempre e sicuramente 1 e quindi non serve memorizzarlo (viene chiamato bit nascosto); in questo modo si guadagna un bit per la mantissa.
Nel caso della precisione estesa però il bit nascosto non esiste; vengono infatti considerati tutti i bit della mantissa partendo quindi dalla notazione normalizzata del valore reale; questo avviene per due motivi:
la mantissa è già abbastanza grande e non serve guadagnare un bit aggiuntivo;
essendo quella estesa la forma usata internamente per i calcoli, è meglio avere memorizzati tutti i bit della rappresentazione dei valori in modo da facilitare le operazioni su di essi.
La notazione quasi normalizzata si ottiene da quella normalizzata spostando di un posto a destra il punto frazionario e togliendo quindi dalla mantissa il primo bit che vale sempre 1 e che diventa la parte intera del valore; questo è il bit nascosto che, come detto, non viene preso in considerazione nei casi di singola e doppia precisione.
Se consideriamo allora l'esempio illustrato alla fine del paragrafo precedente, cioè quello riguardante il valore 5.875, non dobbiamo considerare come punto di partenza per la rappresentazione nello standard IEEE 754 il valore normalizzato 0.1011112*23, bensì il valore quasi normalizzato 1.011112*22.
In questo caso abbiamo dunque che la mantissa è 1.011112 (di cui si memorizza solo la parte frazionaria 011112) mentre la caratteristica è 102.
Nella tabella che segue viene dettagliata la quantità di bit usati, nei tre formati dello standard, per rappresentare il segno, la caratteristica e la mantissa dei valori reali; si noti che le tre informazioni vengono codificate nell'ordine appena enunciato.
|
Una osservazione importantissima deve essere fatta per la caratteristica che viene memorizzata con il metodo dell'eccesso (per risparmiare il bit che servirebbe a rappresentare il suo segno).
Il valore di polarizzazione viene calcolato con la seconda formula tra le due possibili enunciate nel paragrafo (3.1.1.2) riguardante i numeri interi macchina e cioè:
bias = 2(N-1)-1
dove N è il numero di bit da usare.
Quindi la caratteristica viene espressa in eccesso 127 nel caso di singola precisione e in eccesso 1023 nel caso di doppia precisione.
Nel nostro esempio del valore 5.875, abbiamo che la caratteristica rappresentata è 129 (100000012) e 1025 (100000000012) rispettivamente.
Le stringhe complete di bit che rappresentano il valore 5.875 nei formati singola precisione e doppia precisione sono:
0 10000001 01111000000000000000000
0 10000000001 0111100000000000000000000000000000000000000000000000
Gli spazi sono stati messi solo per far comprendere meglio la separazione tra bit del segno, caratteristica e mantissa, ovviamente l'elaboratore non li inserisce nella rappresentazione.
Per avere una forma più compatta delle stringhe appena ottenute, possiamo sostituire ai trentadue o ai sessantaquattro bit, a gruppi di quattro, le corrispondenti cifre esadecimali:
40BC000016
401780000000000016
Consideriamo adesso il procedimento inverso, cioè quello che ci permette di passare da una sequenza di trentadue o sessantaquattro bit al valore reale decimale rappresentato.
Come primo esempio partiamo da una rappresentazione in singola precisione i cui bit corrispondono alle cifre esadecimali 414E000016:
i bit sono quindi:
0 10000010 10011100000000000000000
da cui si deduce che il segno è positivo, la caratteristica rappresentata è 130 e quindi quella effettiva è 3, mentre la mantissa è 1.1001112.
Quindi il valore binario è 1100.1112 che corrisponde a 12.875 .
Vediamo poi la seguente rappresentazione in doppia precisione, sempre con in bit raggruppati in notazione esadecimale, BFE600000000000016:
passiamo a scrivere i bit per esteso:
1 01111111110 0110000000000000000000000000000000000000000000000000
abbiamo quindi segno negativo, caratteristica rappresentata 1022, cioè effettiva -1, mantissa 1.0112.
Il valore binario è dunque -0.10112 che corrisponde a -0.6875 .
I valori estremi della caratteristica (tutti zero o tutti uno) assumono un significato particolare:
se i bit della caratteristica sono tutti zero ed è zero anche la mantissa si rappresenta il valore 0.0;
se i bit della caratteristica sono tutti zero e la mantissa è diversa da zero, siamo in presenza di valori reali denormalizzati (che qui non approfondiamo);
se i bit della caratteristica sono tutti uno e la mantissa è zero si tratta della rappresentazione del concetto di infinito (più o meno infinito, secondo il bit del segno);
se i bit della caratteristica sono tutti uno e la mantissa è diversa da zero si tratta di rappresentazioni non valide («not a number»).
Per precisione di una rappresentazione in virgola mobile si intende il numero di cifre frazionarie che si riescono a rappresentare senza troncamenti.
A tale proposito si osservi che, se si vuole rappresentare in binario con la stessa precisione una mantissa normalizzata in base 10, occorre prevedere un numero di cifre binarie pari a più del triplo delle cifre presenti nella rappresentazione decimale.
Infatti abbiamo osservato nel paragrafo 1.2 sulla misura dell'informazione, come il numero di bit necessari a rappresentare un valore decimale è 3.32 (arrotondato a 4).
Alla stessa conclusione si arriva osservando che il numero di cifre binarie necessarie per esprimere un valore V è proporzionale a log2(V), mentre il numero di cifre decimali necessarie per esprimere lo stesso valore V è proporzionale a log10(V); quindi dobbiamo calcolare il rapporto:
|
|
Se siamo interessati a gestire valori fino alla k-esima cifra decimale (ovvero ad accettare un errore di 10-k), dovremo allora prevedere di usare 3.32*k cifre binarie frazionarie.
Riassumendo si ha che le cifre per la memorizzazione della mantissa servono per la precisione, mentre le cifre per la memorizzazione della caratteristica determinano l'ampiezza dell'intervallo dei valori reali macchina.
A proposito della precisione con cui si possono rappresentare i valori reali macchina, si definisce precisione macchina il valore più piccolo, in valore assoluto, che l'elaboratore è in grado di «apprezzare» nei calcoli; lo si può calcolare con il seguente metodo:
si imposta prec = 1;
si esegue ciclicamente prec = prec/2 finché 1 + prec > 1;
quando 1 + prec = 1 vuol dire che prec non viene più «sentito» nei calcoli e quindi prec = prec * 2 è la precisione di macchina.
|
Si noti che il valore della precisione di macchina è diverso (maggiore) del valore positivo più piccolo rappresentabile; nel caso di singola precisione si hanno rispettivamente i valori: 2.3*10-7 e 1.2*10-38. |
DA COMPLETARE ..........
I calcoli effettuati con i numeri floating-point possono essere affetti non solo da errori (di troncamento/arrotondamento, incolonnamento, cancellazione) sui dati introdotti dal sistema quando le cifre significative sono diverse da quelle ammesse nella rappresentazione, ma anche da errori generati dal particolare algoritmo usato per sviluppare i calcoli stessi.
L'entità degli errori e l'effetto della loro propagazione nei calcoli va tenuta in considerazione.
Infatti in alcuni algoritmi iterativi la propagazione degli errori durante il ciclo dei calcoli può portare ad una situazione di instabilità o inaffidabilità dei risultati (mentre altre volte è il problema stesso che, essendo mal condizionato, può dar luogo ad instabilità).
Ad esempio nel calcolo per passi dell'integrale definito di una funzione, se si sceglie come passo di integrazione un valore troppo piccolo, nell'intento di aumentare la precisione del risultato, può accadere che il valore della variabile non venga mai incrementato (errore di incolonnamento e successivo troncamento) e il programma entri in una situazione di ciclo infinito (loop).
Se n è il valore esatto di un numero e ñ il valore rappresentato, si definisce errore assoluto:
e = n - ñ
e errore relativo:
ε = (n - ñ) / n
In genere si è interessati a minimizzare sia il modulo dell'errore assoluto che dell'errore relativo.
Questi aspetti vengono tenuti in grande considerazione quando si deve usare il sistema di elaborazione per effettuare una grande mole di calcoli scientifici; esiste anche una disciplina apposita denominata correntemente calcolo numerico che studia l'entità e la propagazione degli errori numerici introdotti durante l'esecuzione di istruzioni svolte su valori rappresentati in maniera finita e approssimata, al fine di minimizzarli.
L'insieme dei numeri rappresentabili secondo lo standard IEEE 754 è un sottoinsieme dei numeri razionali, distribuito in modo non uniforme: infatti essi sono estremamente vicini fra loro nell'intorno dello zero e si allontanano sempre di più al crescere del loro valore assoluto.
Per verificarlo calcoliamo la differenza (distanza) tra due numeri contigui posti a diversa distanza dal valore zero considerando di avere mantissa espressa con soli tre bit:
num1 = 0.1002 * 21 num2 = 0.1102 * 21
distano la quantità: 0.012 * 21 (pari a 0,5).
Invece i numeri:
num1 = 0.1002 * 24 num2 = 0.1102 * 24
distano la quantità: 0.012 * 24 (pari a 4).
La tabella seguente riassume i valori rappresentabili nell'elaboratore: nel caso degli interi si ha distinzione in base al numero di bit a disposizione per la notazione in complemento a due, nel caso dei reali si considerano le varianti dello standard IEEE 754.
La terminologia è quella dei tipi dati del linguaggio c, anche se non tutti i tipi elencati sono disponibili con tutte le versioni del linguaggio.
Per i valori reali viene riportato solo l'intervallo positivo, essendo quello per i valori negativi speculare rispetto allo zero.
|
Precisiamo che per ottenere i valori mostrati nel caso dei reali macchina è stata considerata la presenza del bit nascosto e non sono stati presi in considerazione i valori estremi della caratteristica (-127, 128 o -1023, 1024 o -16383, 16384 a seconda del formato considerato) in quanto servono a denotare valori speciali; ad esempio per individuare l'intervallo per la singola precisione consideriamo i valori da 1.0 * 2-126 a 1.11111111111111111111111 * 2127, cioè circa da 2-126 a 2128, ottenendo i valori indicati in tabella.
Passiamo adesso ad occuparci della codifica dei dati alfanumerici, non senza avere esaminato qualche nozione sui codici e le codifiche.
Per codice si intende un insieme di parole che sono associate ad un insieme di oggetti da codificare.
Esistono codici naturali (ad esempio le lingue parlate) e codici artificiali, cioè creati dall'uomo per vari scopi.
Ogni codice è basato su un alfabeto di simboli che sono usati per creare le parole del codice; la codifica consiste nell'associare un oggetto dell'insieme da codificare ad una parola di codice, la decodifica è il procedimento inverso che permette di risalire da una parola all'oggetto corrispondente.
Spesso, creando una certa ambiguità, di denomina codice anche la singola parola di codice; di solito però il contesto in cui i termini sono usati permette di evitare confusione tra gli stessi.
I codici possono essere a lunghezza fissa o a lunghezza variabile rispettivamente se tutte le parole hanno la stessa lunghezza oppure no.
Un esempio di codice a lunghezza variabile è il codice Morse in cui l'alfabeto è costituito dai simboli di «punto» e «linea».
Quando la lunghezza è variabile ci sono problemi nel procedimento di decodifica dovuti al fatto che la lunghezza delle parole non è uniforme; questo è vero anche nel codice Morse dove è stato introdotto il concetto di «pausa» per separare lettere, parole e frasi facendo in pratica aumentare il numero di simboli dell'alfabeto usato in quel codice.
Torniamo adesso brevemente al concetto di misura dell'informazione introdotto nel paragrafo 1.2; avevamo visto come la quantità di informazione veicolata da un supporto o da un messaggio che prevede N configurazioni equiprobabili con probabilità P = 1/N è:
|
|
Definiamo ora il concetto di entropia di una fonte o sorgente di informazione (qui ci interessa la fonte costituita dai simboli che sono alla base di un codice):
|
Si dice entropia la quantità di informazione totale relativa a tutti i messaggi che la sorgente può emettere (o tutte le configurazioni che il supporto può assumere), calcolata come media ponderata, rispetto alle probabilità, delle quantità di informazioni dei messaggi. |
In formula (formula di Shannon):
|
|
L'entropia è massima quando tutti gli N messaggi (o tutte le N configurazioni, o tutti gli N simboli dell'alfabeto) sono equiprobabili con probabilità Pk = 1/N; in tal caso:
|
|
Quindi l'entropia del codice definito con le dieci cifre decimali è:
|
|
Si definisce poi la lunghezza media di un codice, misurata in bit per parola (bit/parola), come:
|
|
dove Qi è la probabilità di una parola di codice e Li la sua lunghezza.
Se le M parole di un codice sono equiprobabili e della stessa lunghezza, la lunghezza media è pari alla lunghezza di una parola:
|
|
Il primo teorema di Shannon afferma che:
«la lunghezza di un codice non può mai essere inferiore all'entropia, cioè: L >= H»
In caso contrario si avrebbero infatti codici ambigui in cui ad una parola di codice corrispondono due o più oggetti dell'insieme da codificare.
Si dice efficienza di un codice il rapporto E = H/L
Tale rapporto può essere al massimo pari a 1 e in tal caso si parla di codice efficiente; se invece è minore di 1 si ha un codice ridondante.
Ad esempio se codifichiamo le sedici cifre esadecimali in binario abbiamo:
L = 4
H = 4
E = 1
Se invece codifichiamo le dieci cifre decimali in binario abbiamo:
L = 4
H = 3.32
E = 0.83
Quindi nel primo caso il codice è efficiente, nel secondo ridondante.
La ridondanza di un codice aumenta ovviamente al diminuire del valore di E.
Esistono, soprattutto riguardo la trasmissione delle informazioni, dei codici che sono volutamente inefficienti (E molto piccola), in quanto prevedono l'introduzione nelle parole di codice di bit aggiuntivi al fine di controllare e, talvolta, correggere errori di codifica e di trasmissione (codici a rilevazione o a correzione di errore); questo argomento non viene comunque qui approfondito.
Il codice BCD (Binary Coded Decimal) è un codice, proposto all'inizio degli anni '60, con il quale si possono codificare i valori decimali.
Vengono usati 4 bit per ogni cifra (quindi il codice è ridondante, secondo quanto mostrato nel precedente paragrafo) e le parole di codice corrispondono alla traduzione in binario delle varie cifre:
|
|
Si dice allora che il codice è ponderato (i bit in ogni parola hanno un peso, nell'ordine da sinistra: 8, 4, 2, 1).
Altri codici simili, utilizzati sempre per codificare i valori decimali sono il codice Stibitz o codice eccesso 3:
|
|
e il codice Aiken: o codice 2421:
|
|
Il primo non è ponderato ma è autocomplementante in quanto per ottenere il complemento a nove di una cifra basta invertire il valore dei bit (questa è una caratteristica importante in quanto le sottrazioni tra due valori si effettuano come somme tra il primo e il complemento a nove del secondo).
Il codice Aiken è sia autocomplemantante che ponderato (con pesi 2, 4, 2, 1, da cui il nome).
Di questi due codici non forniamo qui ulteriori dettagli.
Tornando al codice BCD possiamo osservare che con esso si possono comodamente rappresentare le cifre di un numero in un nibble (4 bit) avendo quindi la possibilità di memorizzare due cifre in ogni byte; in questo caso si parla di Packed BCD.
Il segno del numero decimale viene memorizzato nell'ultimo nibble o nell'ultima cifra con la seguente convezione:
|
Il valore decimale +134.67 viene quindi memorizzato nel seguente modo su tre byte:
0001 0011 0100 0110 0111 1100
Gli spazi sono inseriti solo per migliorare la leggibilità; il punto frazionario non viene memorizzato perché la quantità di cifre frazionarie viene assunta come fissa e nota a priori.
Esiste anche la rappresentazione Zoned BCD in cui ogni cifra viene memorizzata in un byte andando ad occupare il nibble più basso (denominato digit) mentre quello più alto (denominato zonatura) viene riempito con quattro bit fissi che possono essere:
1111, come avviene nel codice EBCDIC;
0011, come avviene nel codice ASCII.
L'eventuale segno viene memorizzato nella zonatura della cifra meno significativa con le rappresentazioni illustrate in precedenza.
Per i codici EBCDIC e ASCII si rimanda al prossimo paragrafo, qui notiamo solo che il vantaggio della rappresentazione Zoned BCD è che i valori numerici vengono memorizzati rappresentando in memoria i simboli decimali corrispondenti alle singole cifre; questo aumenta le chiarezza della rappresentazione dei dati in memoria al prezzo di un notevole spreco di bit (un byte per ogni cifra anziché un byte per due cifre).
I numeri Packed BCD hanno un grosso vantaggio rispetto ai numeri espressi con i metodi visti nel paragrafo 3.1 in quanto si possono rappresentare certi valori con maggiore precisione; ad esempio il numero decimale 12.3 in BCD diventa 00010010.0011 (qui il punto frazionario è stato lasciato per chiarezza di esposizione, ma, come detto, non viene memorizzato).
Lo stesso valore in binario «puro» dovrebbe essere necessariamente approssimato in quanto periodico.
Un altro punto a favore del codice BCD è la facilità della conversione del codice di una cifra nel relativo carattere o nella forma utile alla sua rappresentazione nei display a sette segmenti.
Questo vantaggi hanno fatto si che il codice Packed BCD (e anche lo Zoned BCD) sia stato largamente utilizzato in tutte le applicazioni, come quelle commerciali, in cui c'è l'esigenza di memorizzare e gestire valori con poche cifre decimali ma espressi senza errori di rappresentazione; fra il linguaggi di programmazione il COBOL (COmmon Business Oriented Language) è quello che fa maggior uso di questi sistemi di codifica dei valori numerici.
Gli elaboratori o i linguaggi che prevedono la memorizzazione di valori decimali packed o zoned e che possiedono istruzioni per la loro manipolazione si dicono elaboratori o linguaggi con aritmetica decimale.
Una diffusione maggiore del codice BCD è stata ostacolata da due suoi grossi difetti causati dalla ridondanza:
«spreco» di bit; il numero di bit usati per rappresentare un valore in BCD è in genere maggiore rispetto al numero necessario per rappresentarlo in binario: ad esempio 129 in binario è 100000012 mentre in BCD è 000100101001.
maggiore complessità delle operazioni con necessità di dotare i microprocessori di istruzioni apposite per i valori BCD.
Chiariamo meglio il secondo aspetto con un esempio in cui si sommano i valori 77 e 11, 88 e 4 e 68 e 19 rappresentati in BCD:
|
|
Nel primo caso il risultato è corretto, nel secondo si ha una cifra (quella a destra) «fuori codice» e il terzo risultato è palesemente errato (la causa è che c'è stato un riporto tra le due cifre decimali).
Si rende quindi necessario intervenire con il cosiddetto aggiustamento decimale o correzione decimale che consiste nel sommare il valore 0110 (sei in BCD) alla cifra fuori codice e alla cifra che ha fornito il prestito; se dopo tale procedimento si hanno ancora cifre fuori codice occorre riapplicare ad esse la correzione (non però se si hanno riporti fra cifre decimali durante l'aggiustamento).
Questo modo di operare è giustificato dal fatto che usando quattro bit il riporto non si ha al raggiungimento del valore 10, bensì del valore 16, cioè con 6 unità di ritardo.
Effettuando la correzione decimale alle due operazioni errate si ottiene:
|
|
Vediamo un ulteriore esempio in cui si sommano i valori 423 e 879 in BCD apportando subito le necessarie correzioni decimali:
|
|
La differenza in BCD si effettua come somma del primo operando con il complemento a 10 del secondo operando (scartando la cifra in più a sinistra nel risultato); ad esempio 85 - 49 diventa 85 + 51 e quindi:
|
|
Il codice EBCDIC (Extended Binary Coded Decimal Interchange Code) fu proposto dall'IBM negli anni '60 con l'avvento degli elaboratori della serie 360; non è mai divenuto uno standard ma è stato utilizzato per tutti i grossi elaboratori IBM.
Esso nacque come estensione di un codice della stessa IBM, denominato BCD, che però era diverso dal BCD di cui abbiamo già parlato, in quanto prevedeva parole di sei bit ed era in grado di codificare le cifre decimali, le lettere maiuscole dell'alfabeto inglese e alcuni caratteri speciali o di controllo.
Un altro codice con parole di sei bit, molto famoso e utilizzato in quegli anni era il FIELDDATA degli elaboratori della Univac.
Il codice EBCDIC è a lunghezza fissa ed è efficiente in quanto rappresenta 256 simboli alfanumerici con parole lunghe otto bit; tra l'altro è anche compatibile con il codice Hollerith usato per le schede perforate nei primi decenni dell'informatica.
In ogni parola di codice i due nibble che compongono il byte prendono il nome di: zonatura, quello più significativo, e digit, quello meno significativo; in pratica la zonatura permette di distinguere i tipi di simboli (ad esempio i simboli relativi alle cifre decimali hanno tutti zonatura 1111), mentre il digit di designare i vari simboli all'interno di ogni tipo.
Nel codice EBCDIC si ha prima la codifica dei caratteri di controllo, poi dei simboli di punteggiatura e accessori, quindi delle minuscole, delle maiuscole (ovviamente in ordine alfabetico e infine delle cifre decimali.
Nella figura 3.41 è riportata la tabella EBCDIC.
|
Figura 3.41 |
Il codice ASCII (American Standard Code for Information Interchange) è invece uno standard approvato dallo ANSI (American National Standard Institute) nel 1963 e fatto proprio dalla ISO (International Standard Organization) come ISO 646.
La prima versione dello standard prevedeva parole di codice lunghe sette bit; il bit eccedente nel byte veniva utilizzato come bit di parità per una blanda forma di controllo sulla correttezza dei sette bit della codifica.
Tale bit veniva infatti posto a zero o uno in modo da far risultare pari la quantità di bit impostati al valore uno in ogni byte; in questo modo un errore di rappresentazione o di trasmissione dati in un byte che facesse diventare dispari tale quantità, poteva essere rilevato (il controllo era però inefficace nel caso di due errori sullo stesso byte che si compensavano lasciando pari la quantità di bit con valore uno).
I simboli codificabili in ASCII ISO 646 sono 128 e si suddividono in:
riproducibili, cioè che si trovano sulle tastiere e possono essere stampati a video o su carta;
non riproducibili, o di controllo o non stampabili la cui presenza deriva dall'importanza che buona parte di essi avevano per gestire le telescriventi, apparecchiature molto usate ai tempi della definizione dello standard (comunque molti di questi simboli conservano anche oggi una notevole utilità); essi, a loro volta, si suddividono in:
simboli di trasmissione, ad esempio: STX = Start Of Text (inizio testo) o ACK = Acknowledge (conferma positiva);
simboli di formato, ad esempio: LF = Line Feed (nuova linea), FF = Form Feed, (nuova pagina), CR = Carriage Return (ritorno a capo);
simboli ausiliari, ad esempio: DEL = Delete (cancella carattere), BEL = Bell (emissione di un suono), NUL = Null (carattere nullo).
I simboli non riproducibili nella tabella dei codici ASCII sono i primi trentadue, quelli il cui codice tradotto in valore decimale è compreso tra 0 e 31.
Seguono poi, inframezzati a simboli vari e di punteggiatura, le cifre decimali, le lettere maiuscole e le lettere minuscole.
Si noti che la sequenza è diversa da quella presente in EBCDIC; questo significa che l'ordine «lessicografico» dei dati nel computer prevede la precedenza di stringhe maiuscole rispetto a minuscole in ASCII e il viceversa in EBCDIC; da questo e soprattutto dal fatto che le parole di codice associate ai vari simboli sono diverse, discende che i due codici sono incompatibili.
Il codice ASCII è usato da tutti i produttori diversi da IBM e anche dalla stessa IBM nel caso dei Personal Computer; in figura 3.42 vediamo la tabella dei codici nella quale notiamo che le parole di codice sono lunghe otto bit: si tratta in effetti della prima metà della tabella ASCII estesa contenente gli stessi codici di quella standard ma con un bit a zero in più a sinistra.
|
Figura 3.42 |
Esiste infatti, dal 1985, una versione più moderna del codice ASCII, chiamata ASCII estesa o ISO 8859, in cui la lunghezza delle parole è otto bit.
I simboli codificabili diventano così 256 e questo permette di codificare correttamente le lettere degli alfabeti diversi da quello inglese, latino e swahili (che sono privi di lettere accentate) i soli per i quali è sufficiente la versione a sette bit.
C'è poi la possibilità di inserire nel codice anche molti altri simboli fra cui ad esempio quelli grafici; inoltre la perdita del bit di parità non è importante in quanto il controllo realizzato con esso non era molto sofisticato e affidabile.
L'estensione del codice è stata fatta in modo «intelligente» lasciando inalterati i primi 128 simboli (a parte l'aumento di lunghezza delle parole) in modo da assicurare la «retro-compatibilità» con la versione precedente del codice.
Sono stati poi creati un certo numero di sottostandard, che si differenziano per gli ultimi 96 degli altri 128 simboli (i primi 32 sono ulteriori caratteri di controllo comuni a tutte le varianti dello standard).
Ognuno dei sottostandard è dedicato ad una particolare lingua o a un gruppo di lingue; abbiamo quindi:
ISO 8859-1 (Latin-1 Western European): per le lingue dell'Europa Occidentale e della Scandinavia (quindi anche delle Americhe, dell'Oceania dell'India e altre ex colonie europee);
ISO 8859-2 (Latin-2 Central European): per le lingue dell'Europa centro orientale basate sull'alfabeto latino;
ISO 8859-3 (Latin-3 South European): per maltese, turco e esperanto;
ISO 8859-4 (Latin-4 North European): lingue dei paesi baltici e della Groenlandia;
ISO 8859-5 (Latin/Cyrillic): lingue basate su alfabeto cirillico;
ISO 8859-6 (Latin/Arabic): arabo;
ISO 8859-7 (Latin/Greek): greco moderno;
ISO 8859-8 (Latin/hebrew): ebraico moderno;
ISO 8859-9 (Latin-5 Turkish): come Latin-1 con l'islandese rimpiazzato dal turco;
ISO 8859-10 (Latin-6 Nordic): modifica del Latin-4 per i linguaggi nordici;
ISO 8859-11 (Latin/Thai): linguaggio thai;
ISO 8859-13 (Latin-7 Baltic Rim): aggiunta di caratteri mancanti in Latin-4 e Latin-6;
ISO 8859-14 (Latin-8 Celtic): lingua celtica;
ISO 8859-15 (Latin-9): revisione del Latin-1 con l'introduzione, tra l'altro del simbolo dell'Euro;
ISO 8859-16 (Latin-10 South-Eastern European): definito per alcune lingue tra cui italiano, sloveno, francese, tedesco con il simbolo di valuta sostituito da quello dell'Euro.
Lo standard ISO 8859, con le sue varianti, copre le necessità di molte delle lingue esistenti; rimangono però fuori tutti quei linguaggi che non sono basati su un alfabeto ma su ideogrammi ognuno dei quali può corrispondere ad una parola o addirittura ad una frase.
Per indicare questi linguaggi si usa l'acronimo CJK (Chinese, Japanese, Korean) dai nomi delle lingue più rappresentative in questo ambito.
La soluzione probabilmente definitiva ai problemi di codifica si ha con la creazione, a partire dal 1991, dell'insieme di caratteri UCS (Universal Character Set), standard ISO 10646, meglio noto come Unicode.
Con questo insieme di caratteri si associa ad ogni carattere o simbolo di ogni lingua del mondo un numero intero detto code point o punto di codifica.
L'insieme è in continua evoluzione e attualmente conta molte decine di migliaia di codici: sono considerati tutti gli alfabeti conosciuti, anche quelli «inventati» come il Klingon della serie televisiva Star Trek.
I punti di codifica si indicano di solito con la notazione U+xxxx, con «xxxx» valore esadecimale del codice; ad esempio il simbolo di «marchio registrato» ® si indica con U+00AD e quello del «copyright» © con U+00A9.
Grazie ad Unicode vengono definite anche le regole di composizione in modo da formare nuovi simboli partendo da da due già esistenti (ad esempio õ da «o» e «~»).
Unicode però non specifica come i simboli debbano essere codificati (che è proprio la cosa più importante dal punto di vista del sistema di elaborazione); a questo scopo esistono le codifiche che definiscono le associazioni tra codici e loro rappresentazioni basate su bit.
Le codifiche più importanti e utilizzate sono:
UCS-2 che usa due byte per codificare ogni simbolo ed è utilizzata dal 1995 nei sistemi operativi della Microsoft e dal linguaggio di programmazione Java; non è pienamente retro-compatibile con il codice ASCII perché, sebbene i primi 128 simboli siano gli stessi, la codifica di ogni simbolo occupa il doppio dei bit;
UTF-8 (Unicode Transformation Format 8), utilizzata nei sistemi Unix e Linux e riconosciuta come standard per le comunicazioni in Internet; è retro-compatibile con ASCII perché i primi 128 simboli, oltre ad essere gli stessi, sono codificati con parole di 8 bit; gli altri codici sono più lunghi (fino a sei byte) e quindi siamo in presenza di una codifica a lunghezza variabile, più complessa da gestire.
La cifra 8 che appare nel nome significa che la base della codifica è il byte (8 bit); esistono anche UTF-7, UTF-16 (estensione di UCS-2) e UCS-4 ma sono molto meno utilizzate.
Come detto, in UTF-8 i primi 128 simboli sono codificati con un byte; quelli da 128 a 2047 invece con due byte (e sono i simboli sufficienti a coprire tutte le lingue occidentali) mentre i simboli da 2048 a 65535 occupano tre byte (ideogrammi e altri simboli vari).